Heartwarming Tips About Tangent Line Of A Linear Function Chart Matlab

Among all functions, linear functions are simplest.

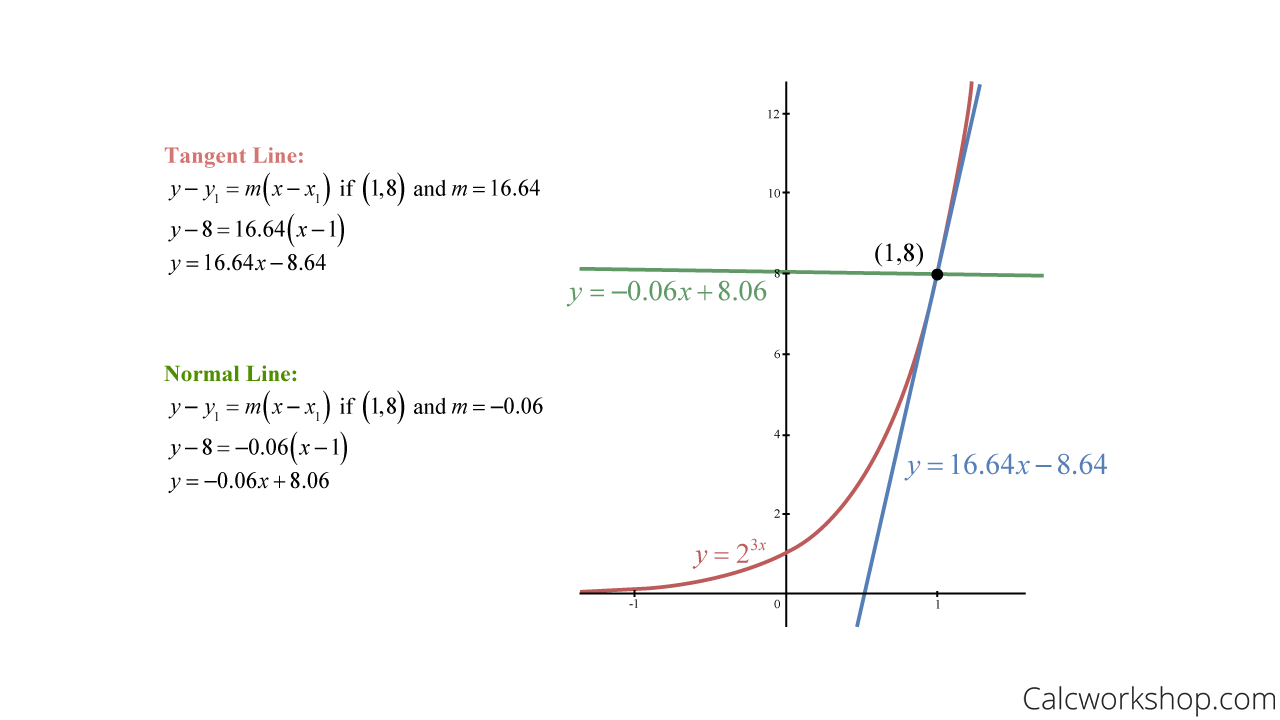
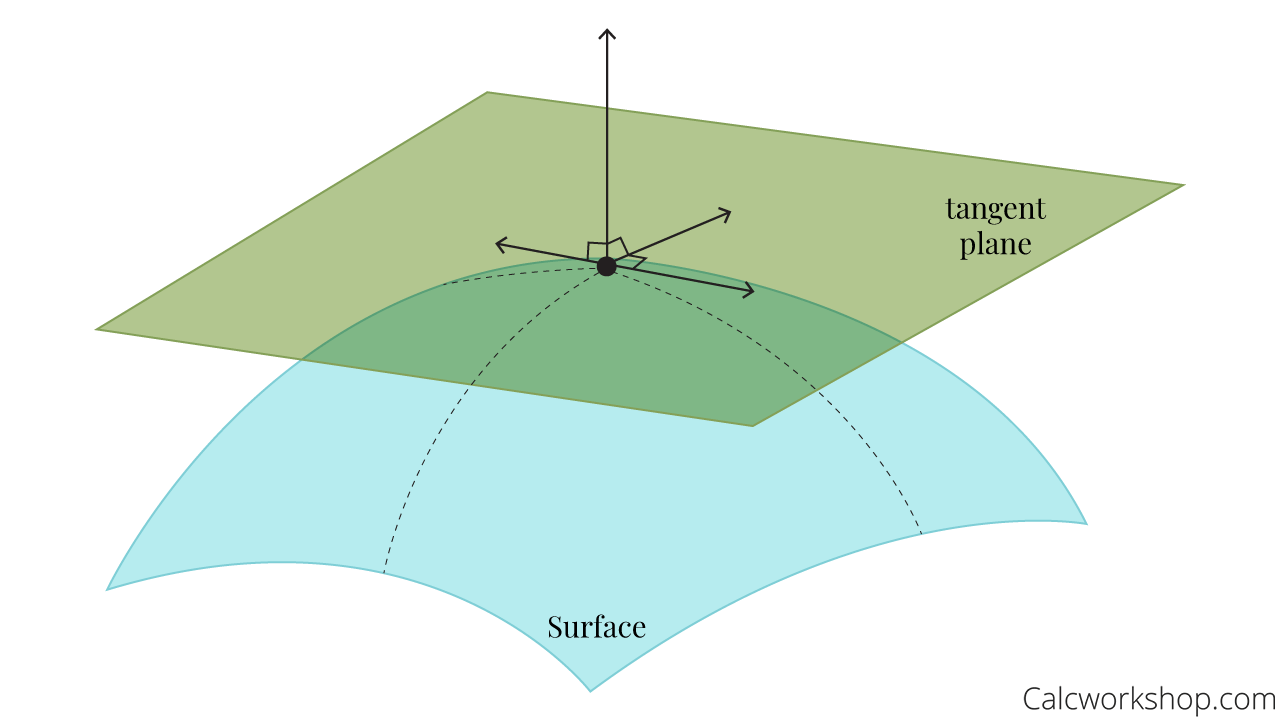
Tangent line of a linear function. The slope of the tangent line is equal to the slope of the function at this point. Linear approximation given a function \( z=f(x,y)\) with continuous partial derivatives that exist at the point \( (x_0,y_0)\), the linear approximation of \(f\) at the point \( (x_0,y_0)\) is. Enter the equation of a curve and coordinates of the point at which you want to find the tangent line.

It is almost like the line is hugging the curve, so they are touching but not merging. We can find the tangent line by taking the derivative of the function in the point. Tangent lines, linear approximation, and newton’s method

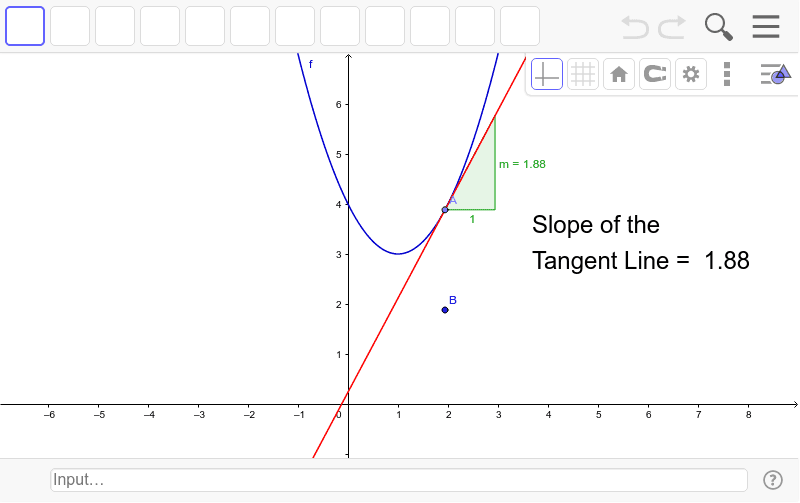
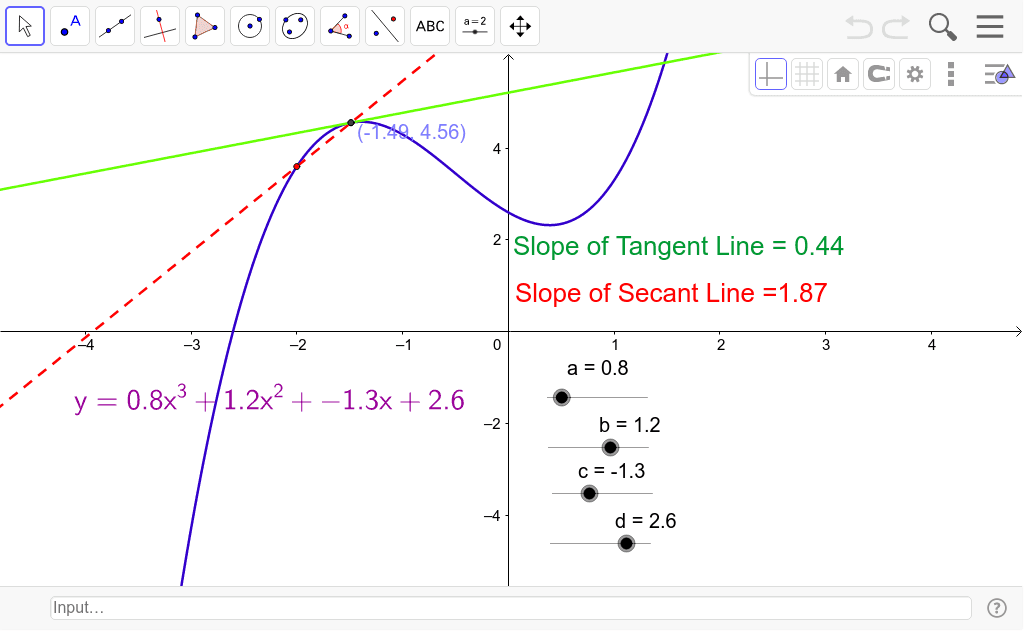
To find the equation of the tangent line in the direction of →v, we first find the unit vector in the direction of →v: The line that touches the curve at a point called the point of tangency is a tangent line. Graph both a function and its tangent line using a spreadsheet or your favorite software.

The tangent line can be used as an approximation to the function f (x) f (x) for values of x x reasonably close to x = a. Derivatives don't have to be linear to still give us the slope of the tangent line. This formula comes in handy when you need to sketch the behavior of the curve near (a) or when analyzing instantaneous rates of change.

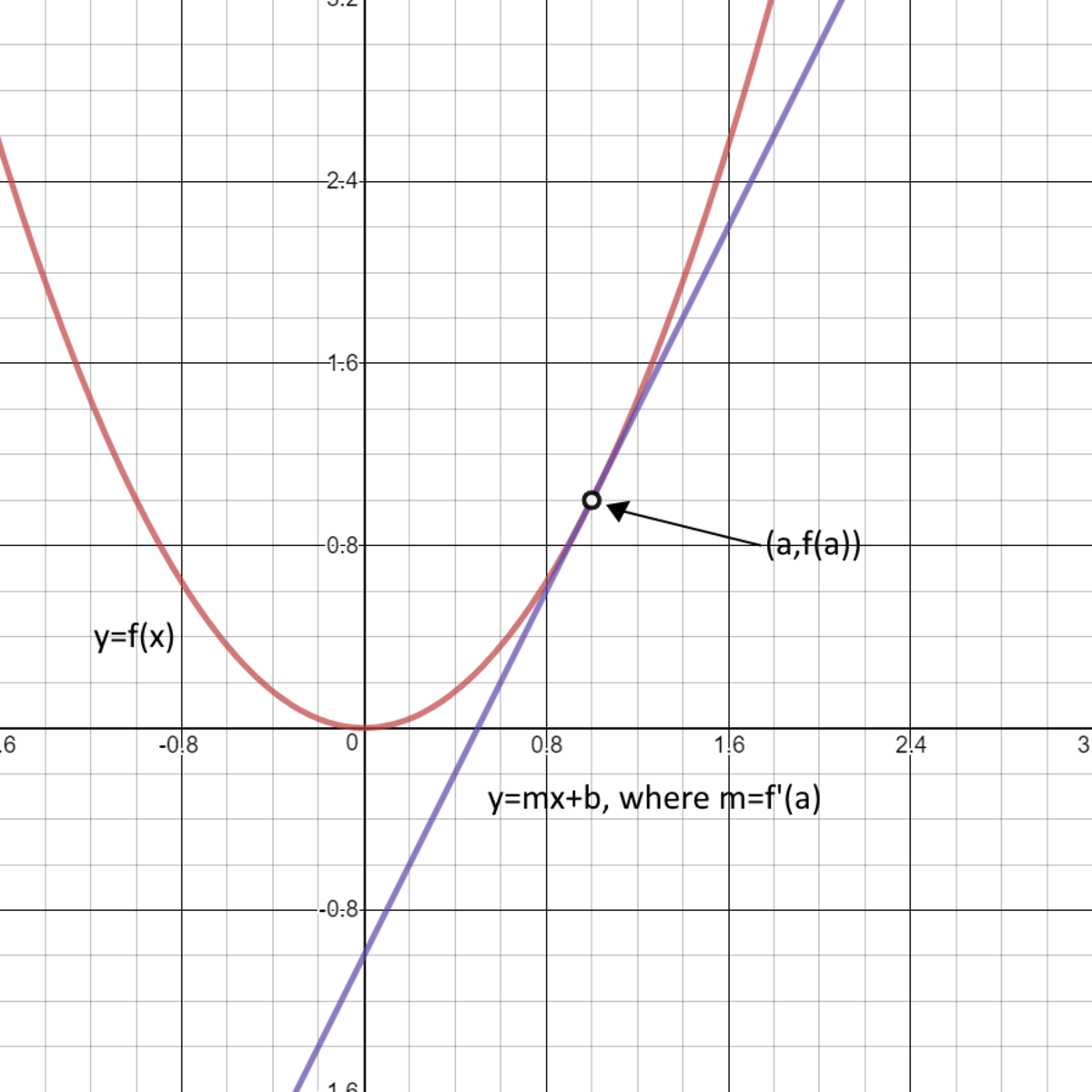
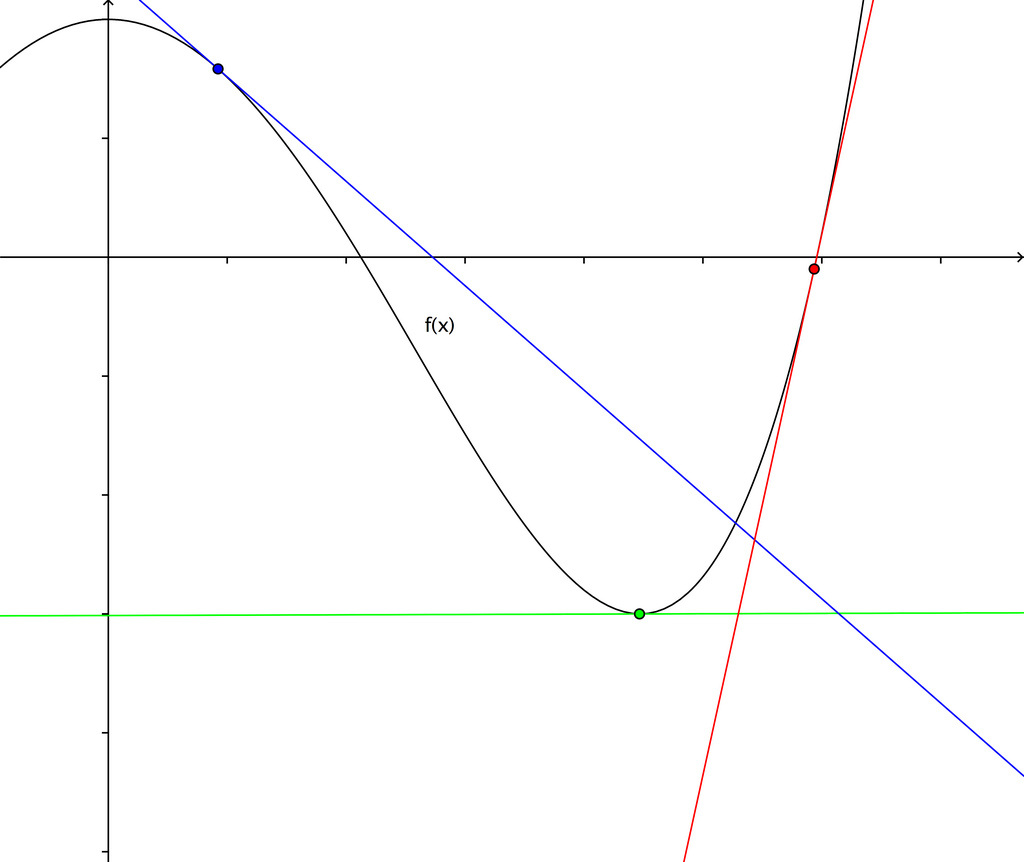
A surface and directional tangent lines in example 12.7.1. A tangent line to the function f(x) at the point x = a is a line that touches a curve at a single point without crossing or intersecting the curve at that point. Given a simple function y = f(x) and a point x, be able to find the equation of the tangent line to the graph at that point.

We can calculate the slope of a tangent line using the definition of the derivative of a function f ‍ at x = c ‍ (provided that limit exists): Take a look at the graph below. Take a look at the graph to understand what is a tangent line.

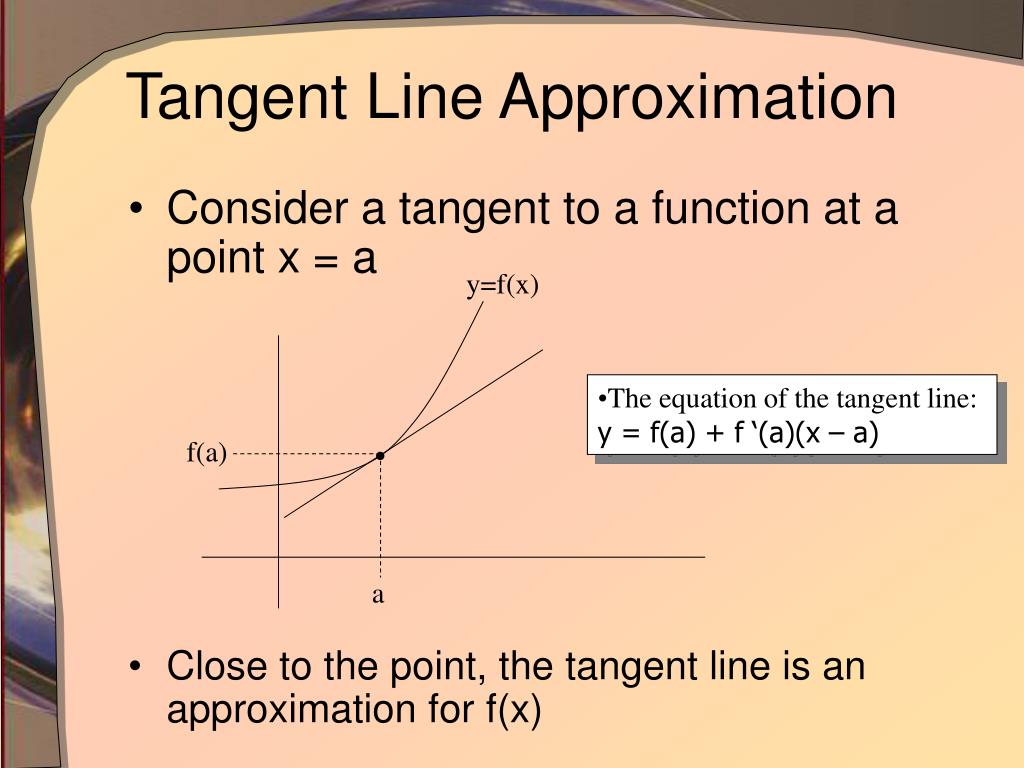
Example of tangent line approximation. Take the derivative of the parabola function to get its slope (don’t let the “letters” scare you): A curve that is on the line passing through the points coordinates (a, f (a)) and has slope that is equal to f’ (a).

The tangent function can be expressed as the ratio of the sine function and cosine function. The equation of the tangent line of a function y = f(x) at a point (x 0, y 0) can be used to approximate the value of the function at any point that is very close to (x 0, y 0). One of the powerful consequences of a function \(y = f (x)\) being differentiable at a point \((a, f (a))\) is that, up close, the function\(y = f ( x )\) is locally linear and looks like its tangent line at that point.

The equation of the parabola so far is $ y=a { {x}^ {2}}+bx+1$. (the result is equation (5.1).) figure 5.4: The tangent function is one of the basic trigonometric functions and is quite a commonly used function in trigonometry.

Use the tangent line approximation to find the approximate value of ∛8.1. The tangent line of a function is always defined relative to a point on the curve. A tangent line to the function f (x) f ( x) at the point x = a x = a is a line that just touches the graph of the function at the point in question and is “parallel” (in some way) to the graph at that point.