Best Of The Best Info About What Is Curve Sketching Used For In Real Life How To Add A Secondary Axis Excel 2010
A function can increase between two points in different ways, as shown in figure.
What is curve sketching used for in real life. We can make a fairly accurate sketch of any function using the concepts covered in this tutorial. They have discontinuities or other unusual. Explain the concavity test for a.
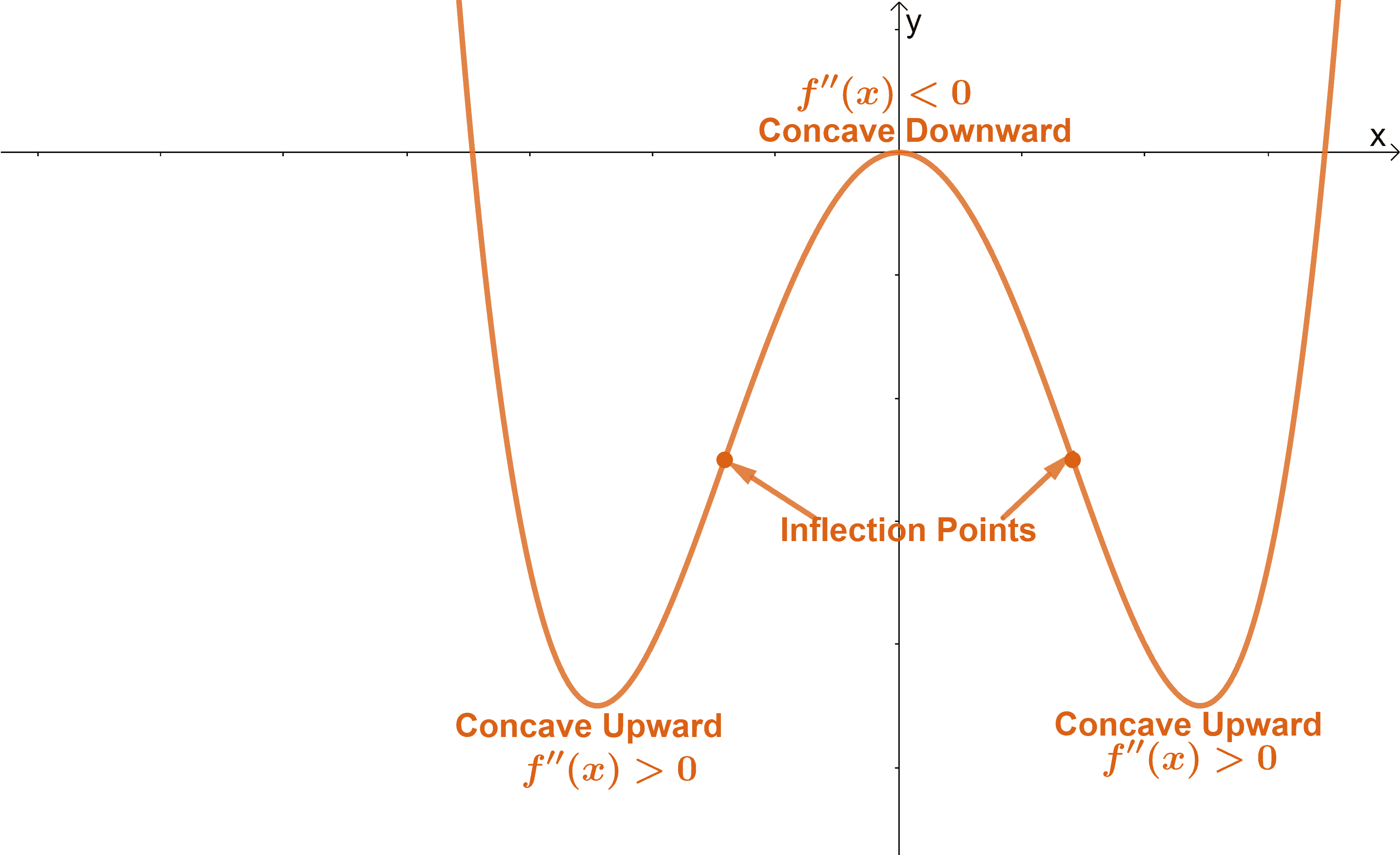
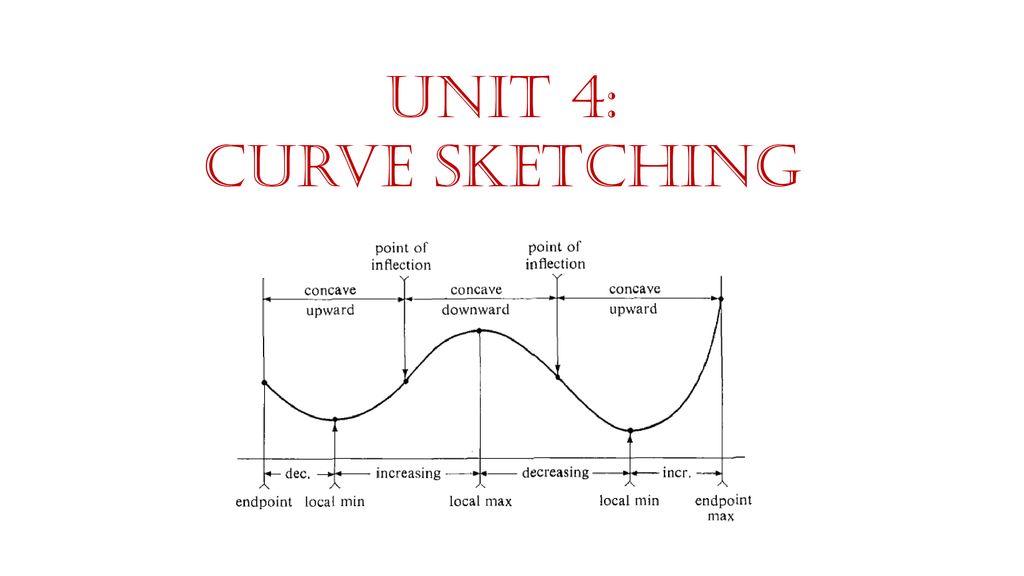
We can use the second derivative of a function to determine. Curve sketching is the process of using algebra and calculus to find the features of a function and then plotting those features in order to draw the function on a. We can use the first derivative of a function to determine regions where a function is increasing vs.
It is an application of the theory of curves to find their main features. Curve sketching is another practical application of differential calculus. Whether we are interested in a function as a purely mathematical object or in connection with some application to the real world, it is often useful to know what.
Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. Sal sketches a graph of f (x)=3x⁴. Conic section is a curve obtained by the intersection of the surface of a cone with a plane.
Whether we are interested in a function as a purely mathematical object or in connection with some application to the real world, it is often useful to know what the. To sketch the graph of f(x), you will. The only critical numbers for \(f\) are \(x = 1\) and \(x = 3\), and they divide the real number line into three intervals:
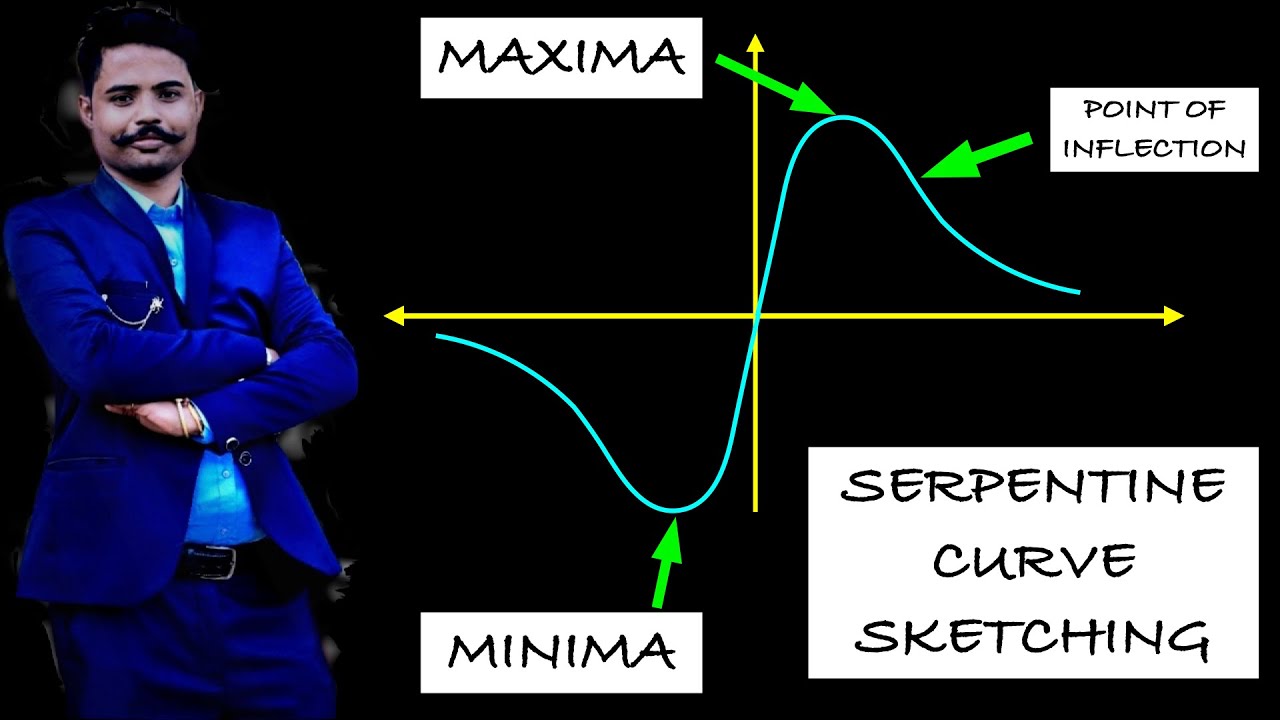
This section deals with curves which are not polynomials. Curve sketching allows us to graph functions using their key properties and its first and second derivatives. Sketching curves of functions and their derivatives.
Curve sketching 2: We have shown how to use the first and second derivatives of a function to describe the shape of. Not only do critical domains of engineering make use of curve sketching, it also aids in understanding.
Analyze a function and its derivatives to draw its graph. January 20, 2013 gb high school algebra, high school mathematics. In analytical geometry, a conic is defined as a plane algebraic curve of.
In figure \ (\pageindex {2c}\) we show a graph of \ (f\) drawn with a. In geometry, curve sketching (or curve tracing) are techniques for producing a rough idea of overall shape of a plane curve given its equation, without computing the large numbers of points required for a detailed plot.