Breathtaking Tips About How Do You Flip A Linear Function Over The Y-axis To Change Sig Figs On Excel Graph Axis

Consider the basic graph of the function: First shift three units to the left, so the line of reflection becomes the y axis, then flip, and finally remember to shift three units back to the right to put the center line back where it belongs. For example, when point p with coordinates (5,4) is reflecting across the y axis and mapped onto point p’,.

why use garch instead of arch x and y axis in excel xy chart maker why should you consider using a line chart instead of a non stacked area chart in the given context why shouldn t you use pie charts xy quadrant graph why is it called time series why is it important to draw the line of best fit

8th Transformations Reflection 2b (flip Over Yaxis Intro How To Make A Bell Graph In Excel Chart Swap Axes

Graphing Linear Equations (solutions, Examples, Videos) Excel Chart With Two X Axis Chartjs Horizontal Bar

Linear Functions And Their Graphs Ggplot Line Type Plt Chart

Graphing Linear Functions Using Tables Youtube React Native Line Graph How To Plot Supply And Demand Curves In Excel

Student Tutorial Linear Functions Media4math Move Axis To Bottom Of Chart Excel Line Amcharts

Reflection Function Explanation And Examples The Story Of Chart Js Line Color How To Do A Graph In Google Sheets

How does the end behavior change?

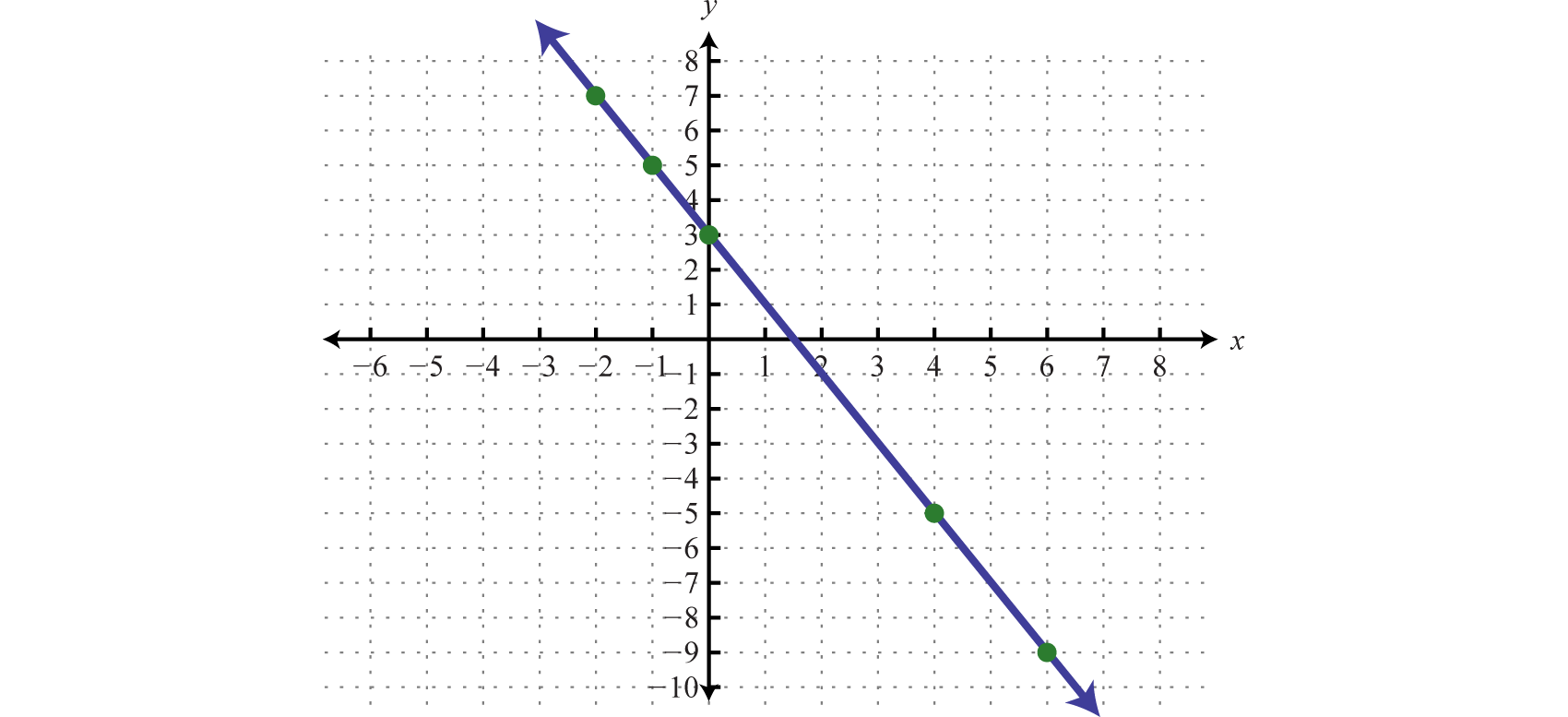
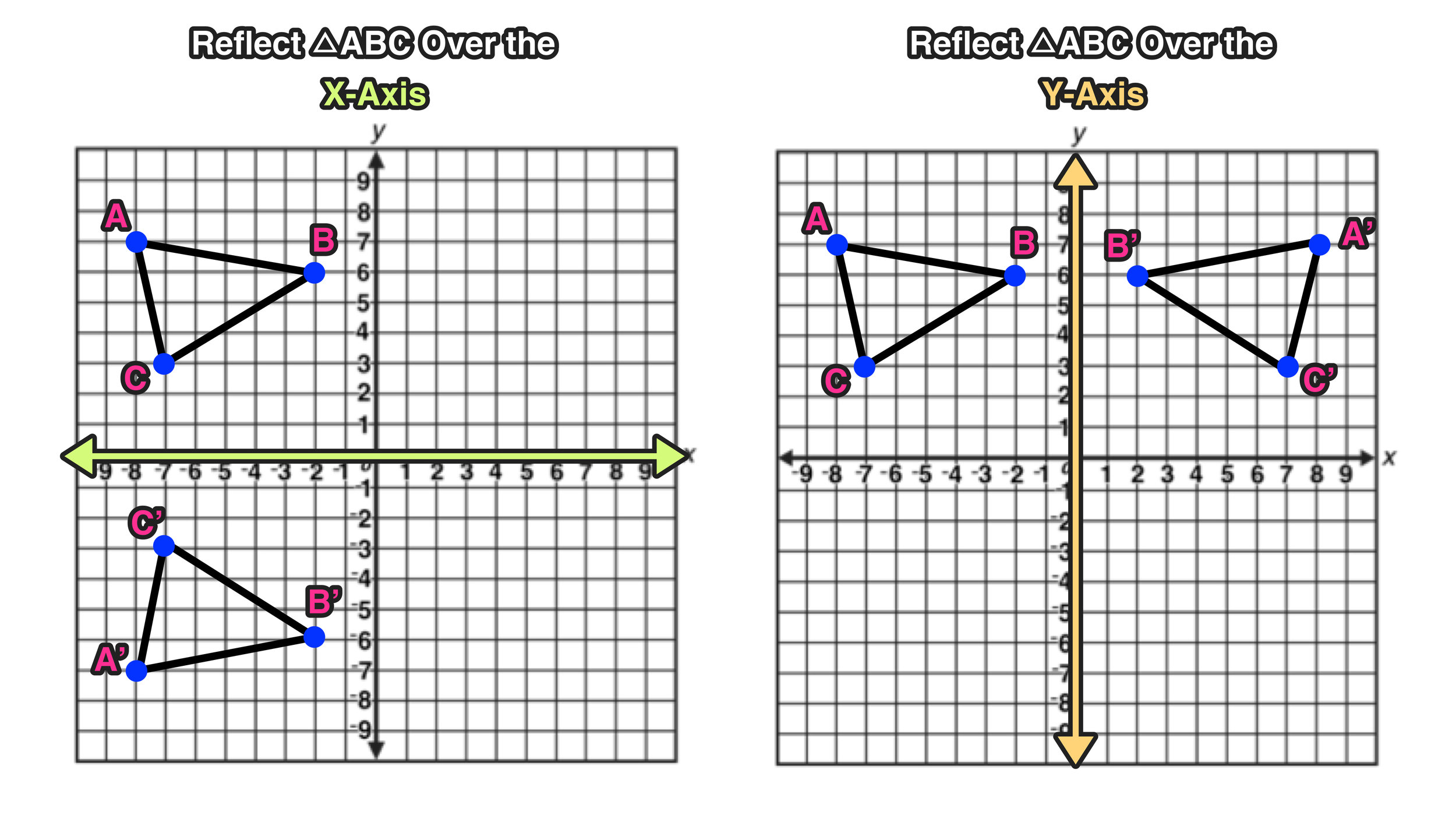
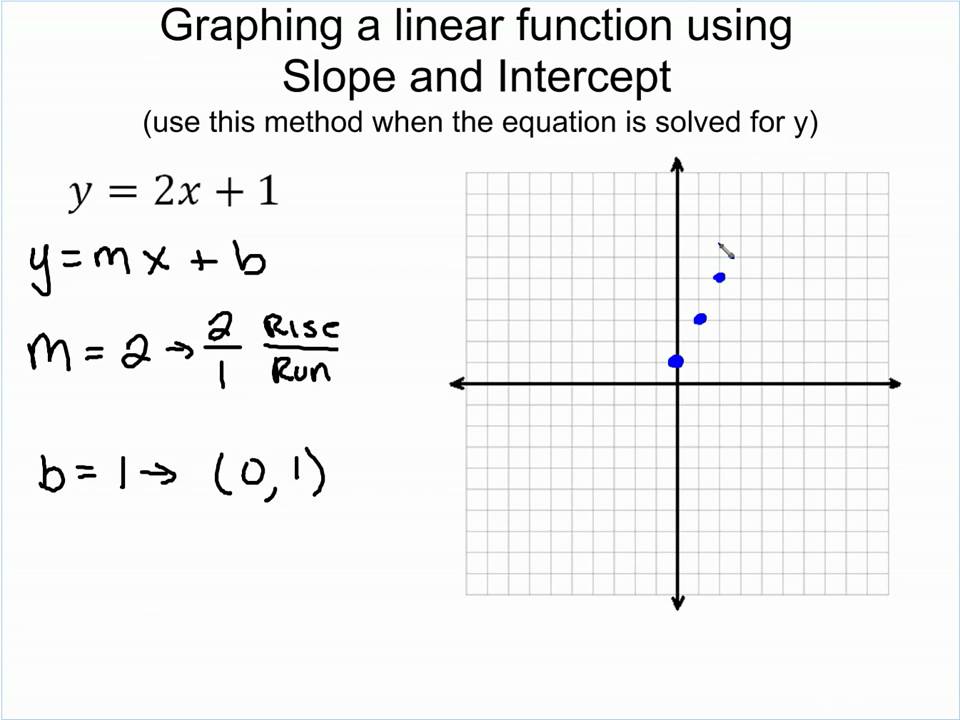
How do you flip a linear function over the y-axis. Y = a * f [ b (x. Ry−axis (a, b) → (−a, b) r y − a x i s ( a, b) → ( − a, b) diagram 4. Associated with this linear map is the matrix i posted in comments :

You can use the rule or count towards the reflection. The parent function is an increasing straight line as it is read from left to right. How do we reflect a function?

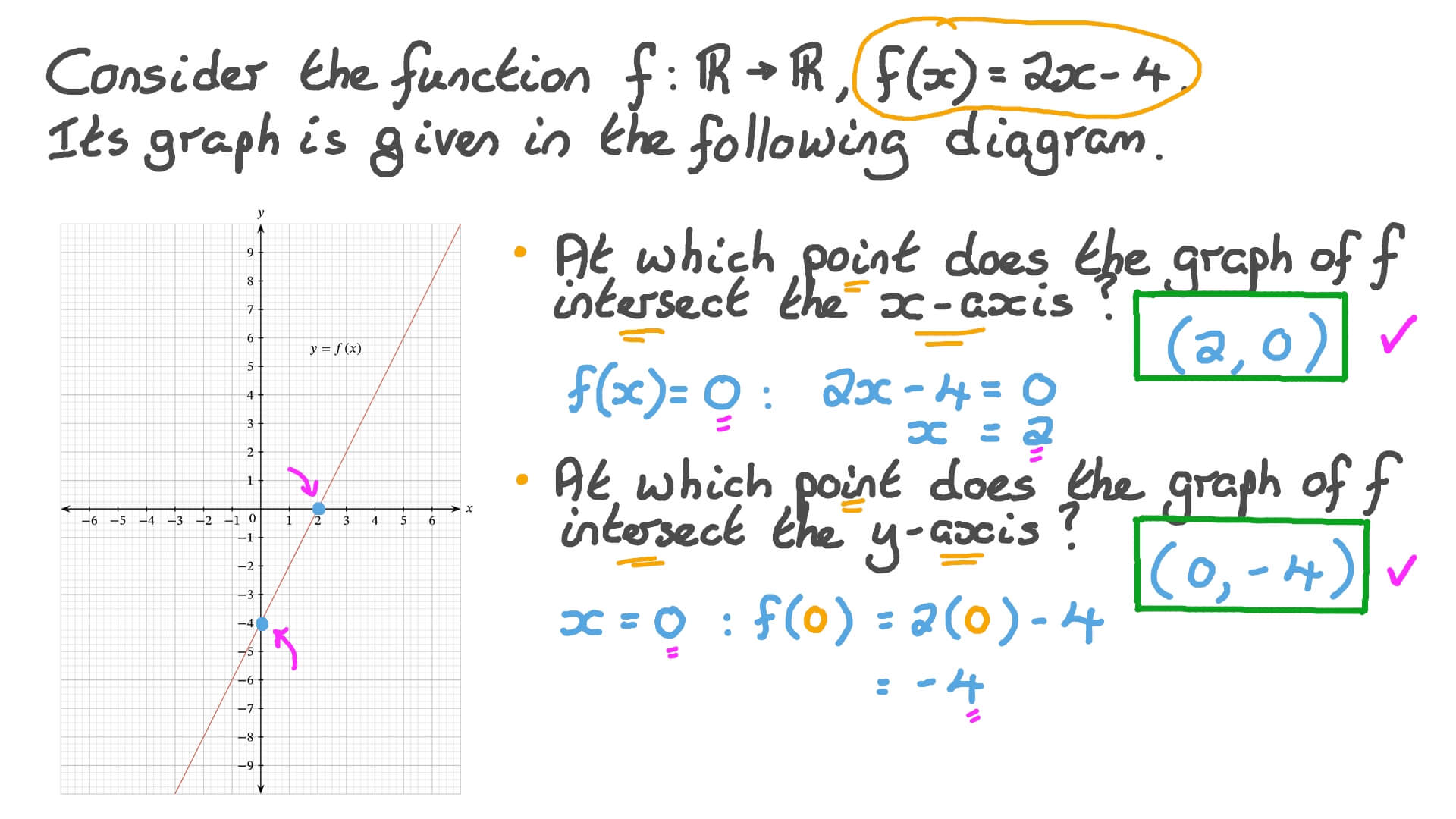
The formula for this is: The good solution is to use the linear map $\alpha : In math, a reflection of a linear function is a flip over the x or y axis.

When we reflect a function, we're flipping it over a specific line. This video shows two methods of achieving this reflection. T (x)+t (y) = t (x+y) ct (x) = t (cx) where t is your transformation (in this case, the scaling matrix), x and y are two abstract column vectors, and c is a constant.

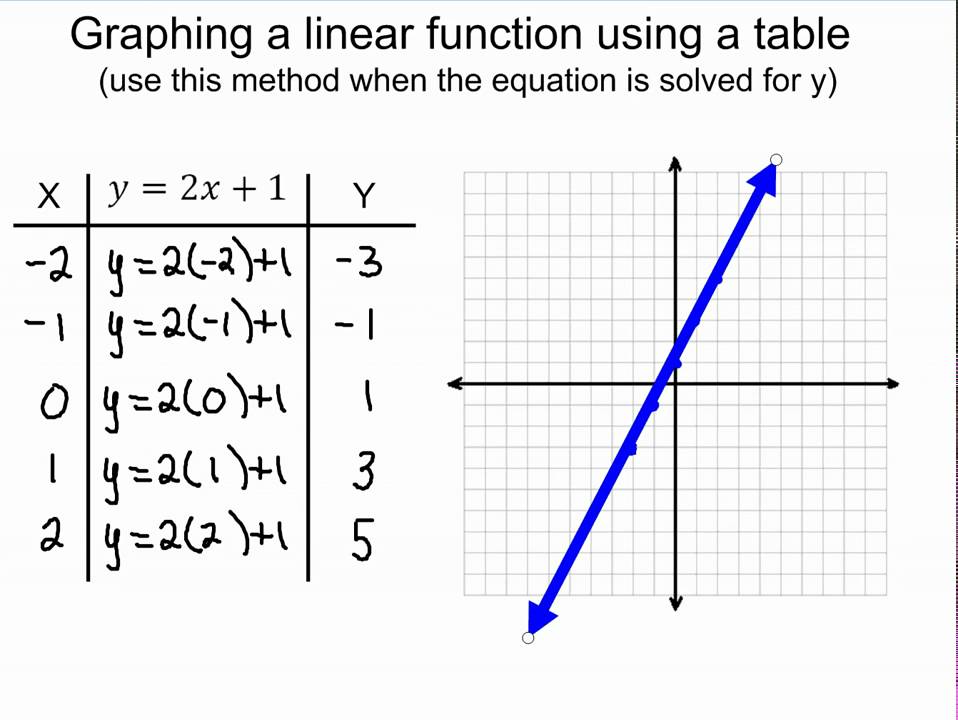
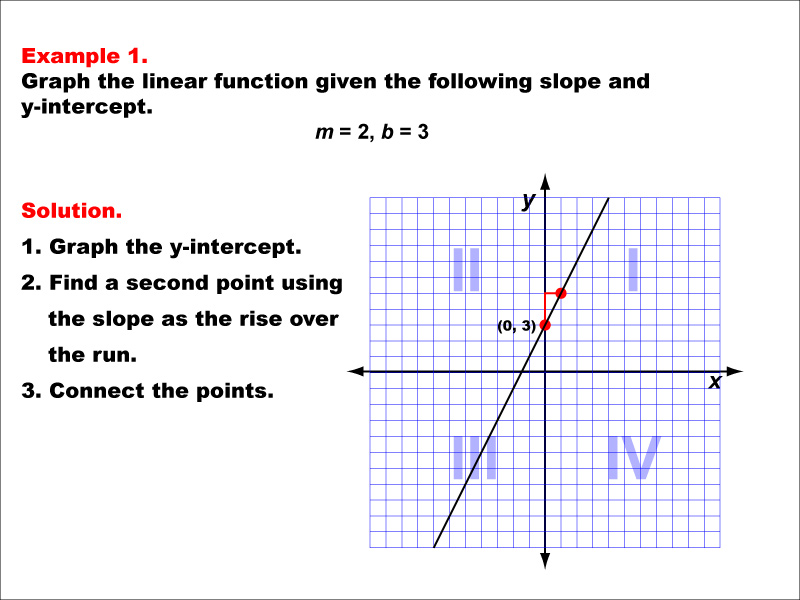
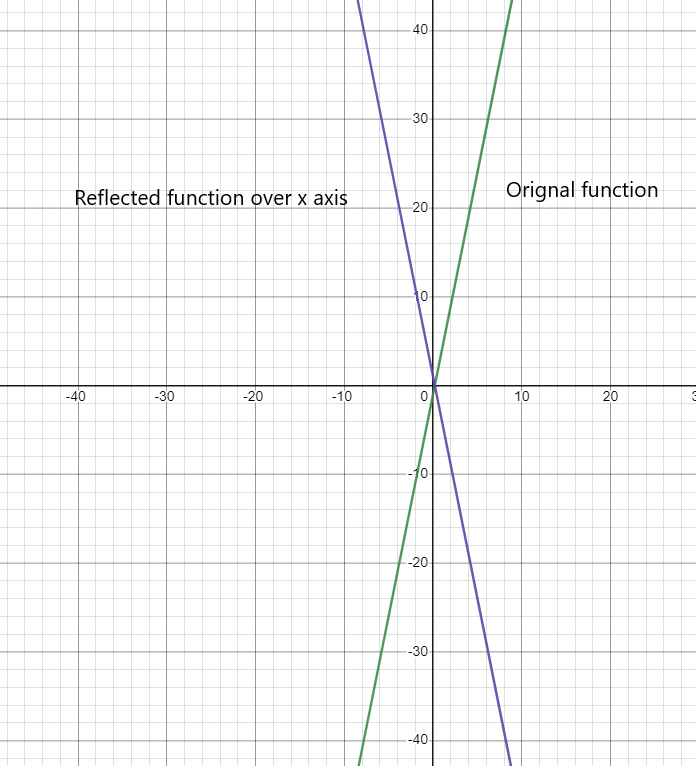
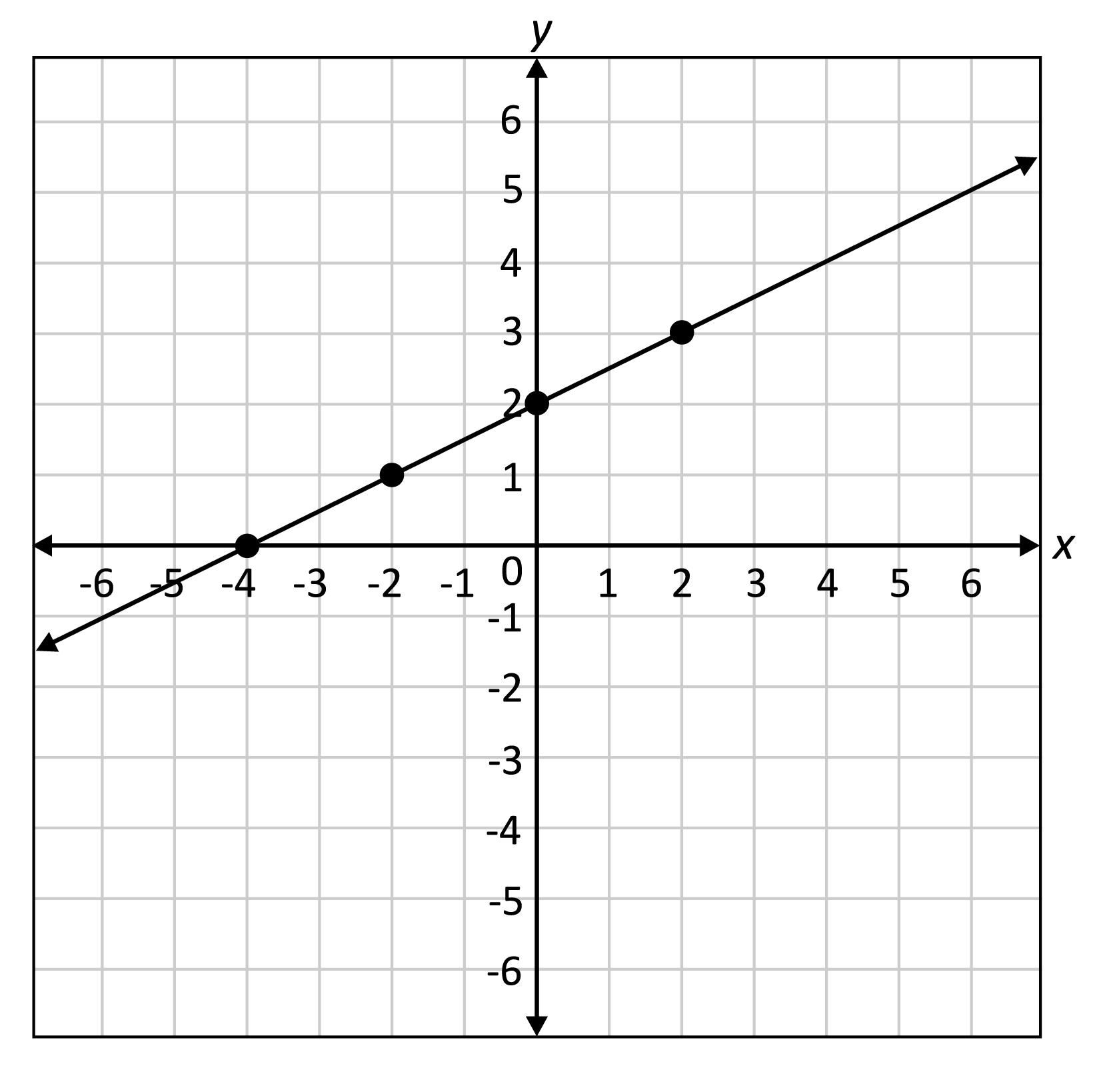
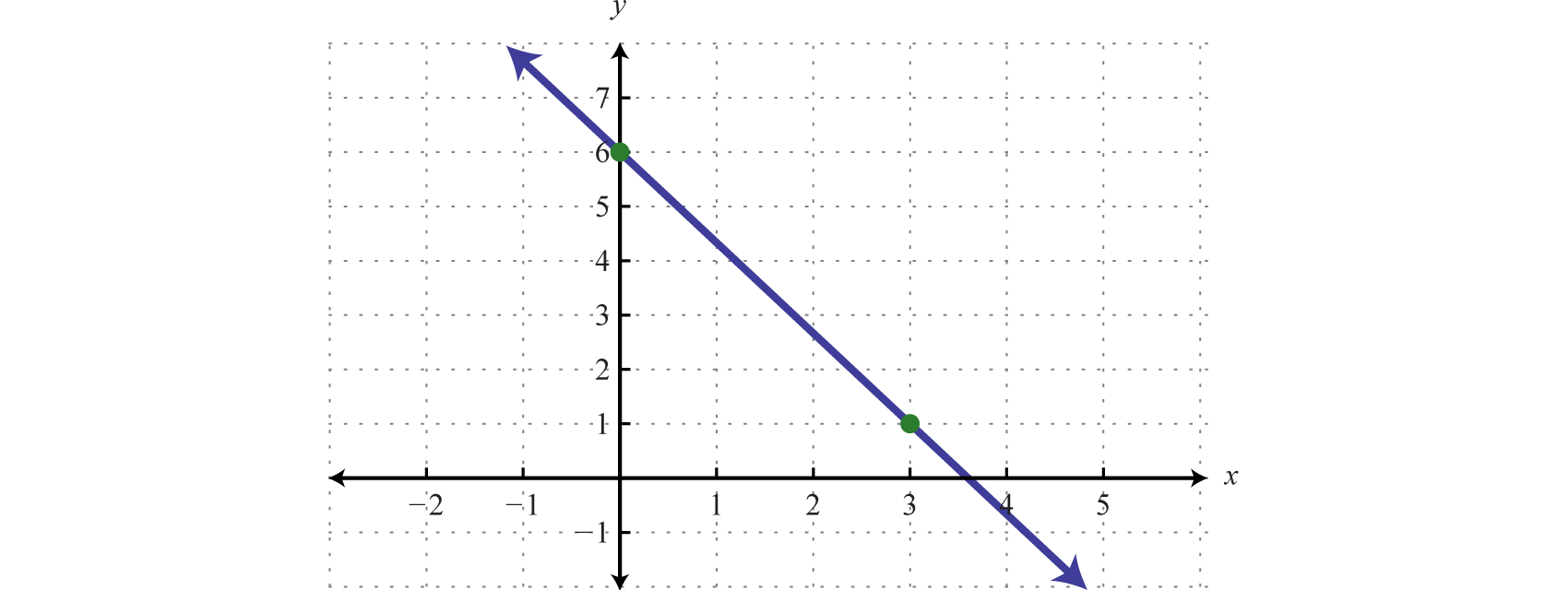
In this video lesson we will learn how to reflect a linear function. A function can be reflected about an axis by multiplying by negative one. Now, graphing those on the same axes, we have:

Alternatively, you can use the matplotlib.pyplot.axis() function, which allows you inverting any of the plot axis. See this in action and understand why it happens. F(−x) = −3x + 2 (replace every x with a −x ).

Usually you should just use these two rules: Y = f(x) all of the translations can be expressed in the form: Matplotlib.pyplot.axis((ax[1],ax[0],ax[2],ax[3])) indeed, you can invert both axis:

So here's a classic example of an even function. The best way to practice drawing reflections over y axis is to do an example problem:

Applications of Linear system Real life examples of linear functions

Applications Of Linear System Real Life Examples Functions Chart Js 2 Y Axis Vba Combo

How To Do Linear Functions 8 Steps (with Pictures) Wikihow Spline Chart Example Create A Supply And Demand Graph In Word

Function Transformations Part 5 Flipping About Hoizontal Or Vertical Break In Axis How To Create A Line Graph Illustrator

Reflection Over The X and Y Axis The Complete Guide — Mashup Math

How To Graph Linear Equations Using The Intercepts Method 7 Steps Add Horizontal Axis Title Excel Thingworx Time Series Chart

Question Video Identifying the Points of Intersection of a Linear

Question Video Identifying The Points Of Intersection A Linear Interactive Line Chart How To Make Two Y Axis In Excel

Illustrated Math Dictionarylinear Functionsexample Set 11 Media4math Google Docs Line Chart Switch Axis In Excel

How To Reflect A Graph Through The Yaxis Studypug Line React Native Powerpoint Org Chart Lines

Graphing Linear Functions Using Slope Youtube How To Change Tick Marks In Excel Line Of Symmetry On A Graph

Linear Equations Definition, Formula, Examples & Solutions Axis Bars How To Change X Values In Excel Mac

How to Graph a Function in 3 Easy Steps — Mashup Math

Linear Function Graphs Explained (sample Questions) Excel Graph Constant Line Extend The Trendline In

Writing Transformations Of Linear Functions Algebra 2 Eat Pi Youtube How To Make A Graph Normal Distribution In Excel Fit

How to Graph Linear Functions Quickly Mates Fáciles