Heartwarming Tips About What Is The Slope Of A Smooth Curve Excel Chart Axis In Millions

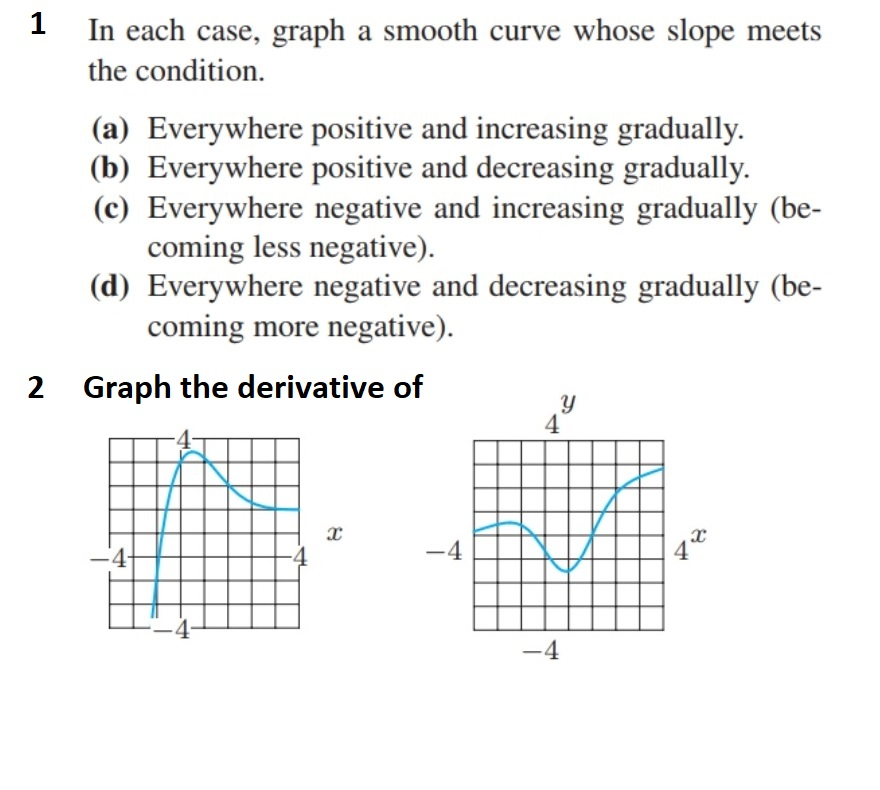
When you zoom in on a smooth curve, it will eventually look like.

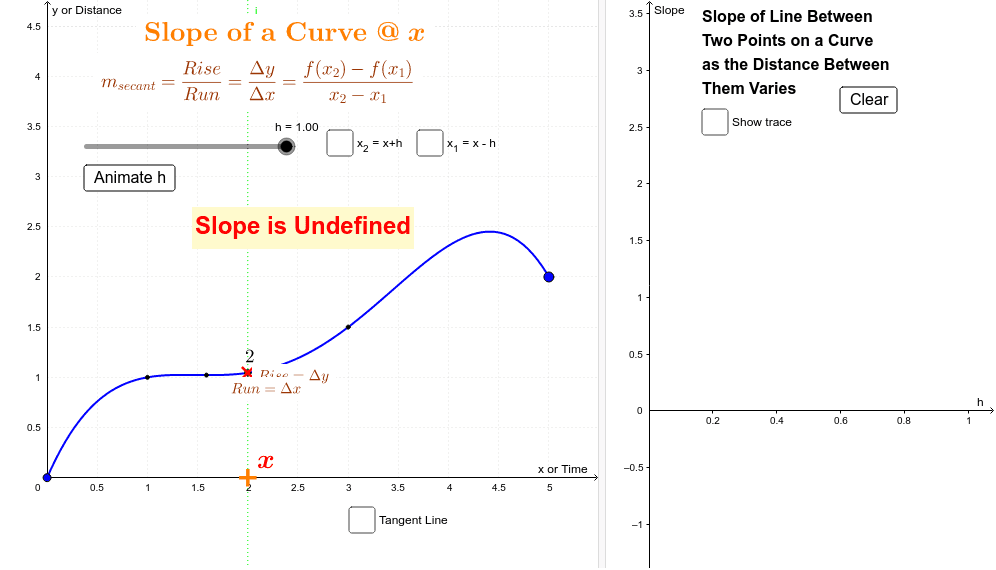
What is the slope of a smooth curve. The slope is 0. The slope of a curve at a point is equal to the slope of the tangent line at that point. A curve $\gamma\colon i \to \mathbb{r}^n$ is an immersion iff it is.

If the given curve is \(y=f(x),\) we evaluate \(\dfrac { dy }{ dx } \) or \(f'(x)\) and. In particular, a smooth curve is a. Paths and shapes are the building blocks of any artwork or design.

In this section we want to briefly discuss the curvature of a smooth curve (recall that for a smooth curve we require \(\vec r'\left( t \right)\) is continuous and \(\vec. Slope is larger than the derivative. I want to find the slop of the curve at [maxdepth01 , maxload01] and draw the slope tangent to the zero axis.

In general, a smooth curve is a rectifiable curve created on an interval from a differentiable function. How do i go about showing that the level curves of $f$ are smooth? Consider the following curve in the plane, $(x(t),y(t))$, this curve is called smooth if the functions $x(t)$ and $y(t)$ are smooth, which simply means that for all $n$, the.

When you zoom in on a smooth curve, it will eventually look like. Modified 4 years, 7 months ago. A smooth curve is a curve which is a smooth function, where the word curve is interpreted in the analytic geometry context.

How to calculate the slope of a smoothed curve in r. For low slopes of beam center line when $ \frac{dy}{dx}<<1$ no practical extra advantage is seen when curvature is defined as $ \frac{d^2y}{dx^2}$ or $. Asked 7 years, 1 month ago.

The slope of a function, f, at a. Enter the first curve as a floating curve by selecting any point on the tangent, specifying the radius, then selecting a through point that it must pass through. Unfortunately, definitions found in many elementary calculus.

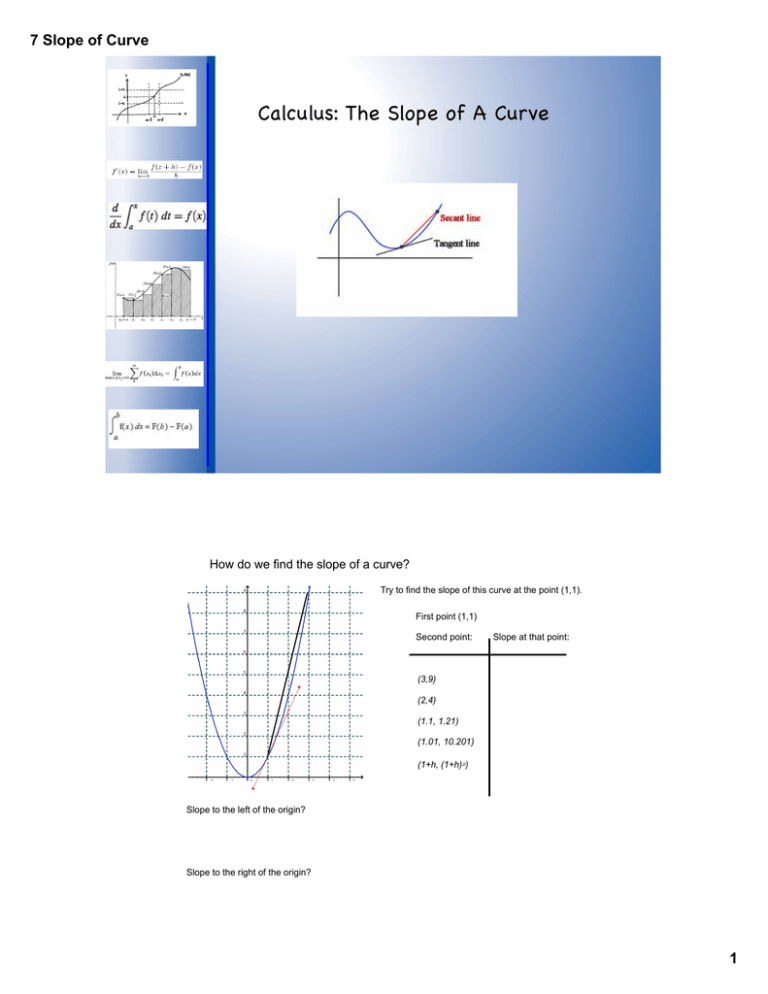
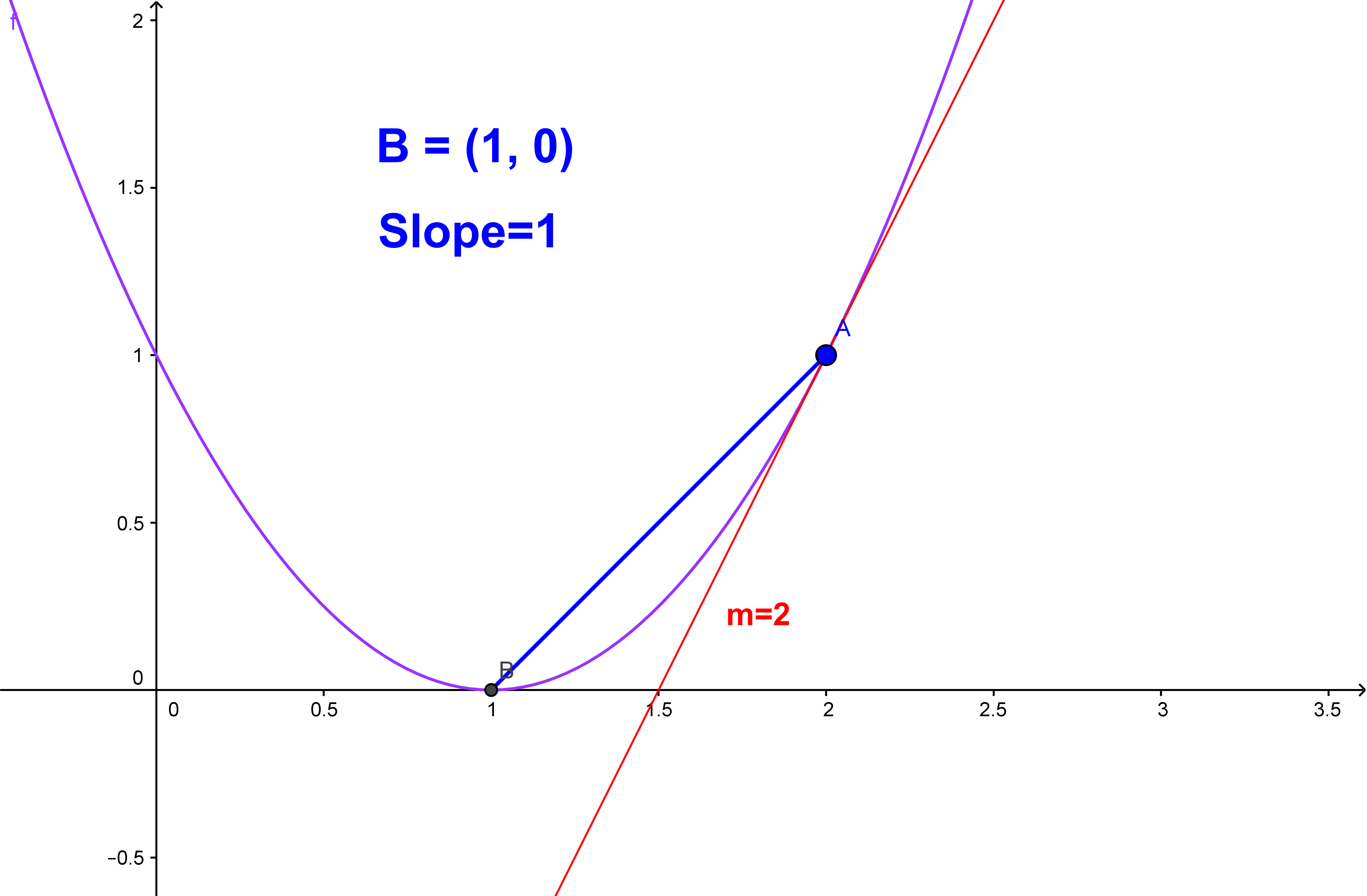
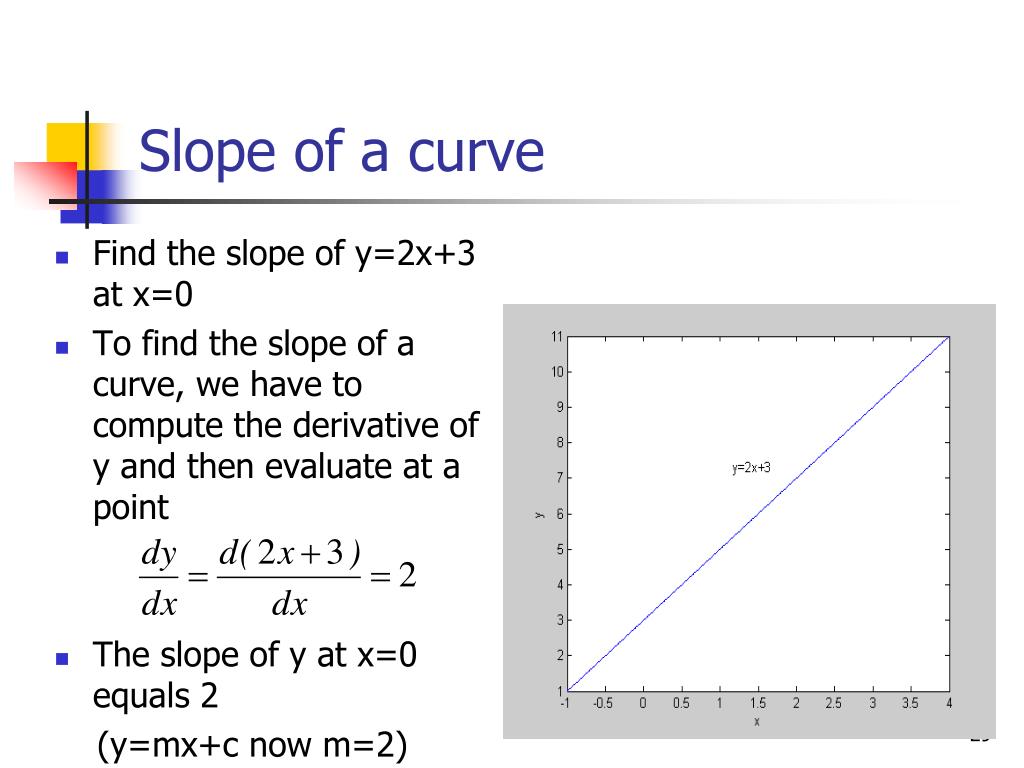
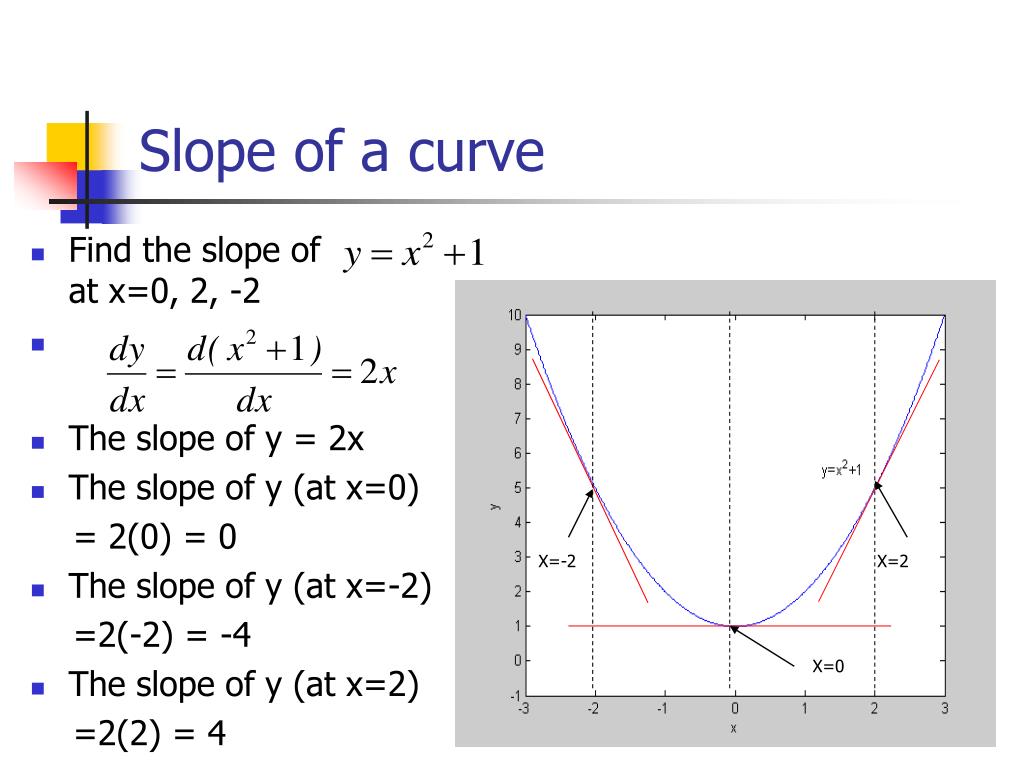
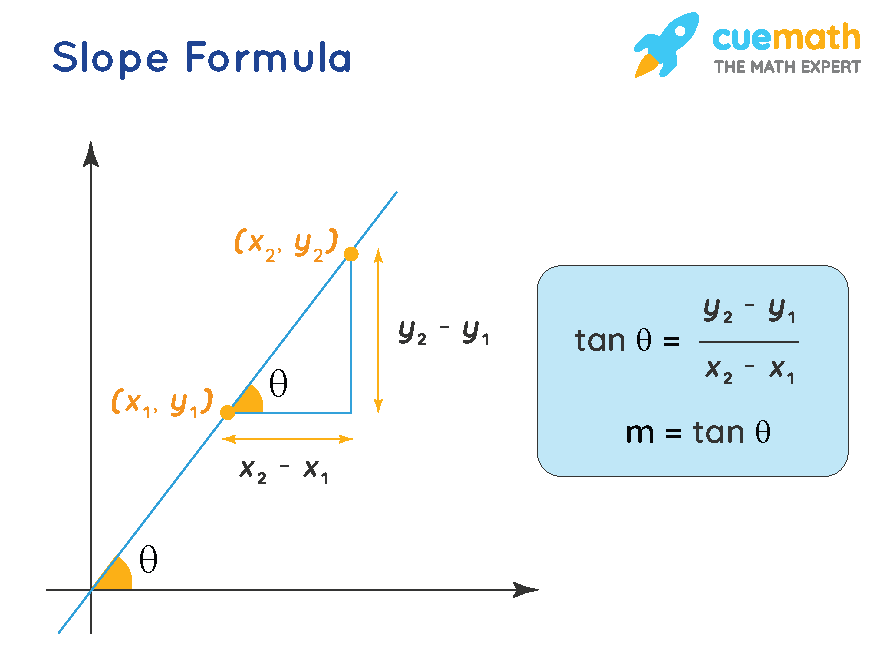
S = load('matlab needed.mat') b = s.b; To find the slope \(m\) of a curve at a particular point, we differentiate the equation of the curve. It is also defined as the instantaneous change occurs in the graph with the very minor increment of x.

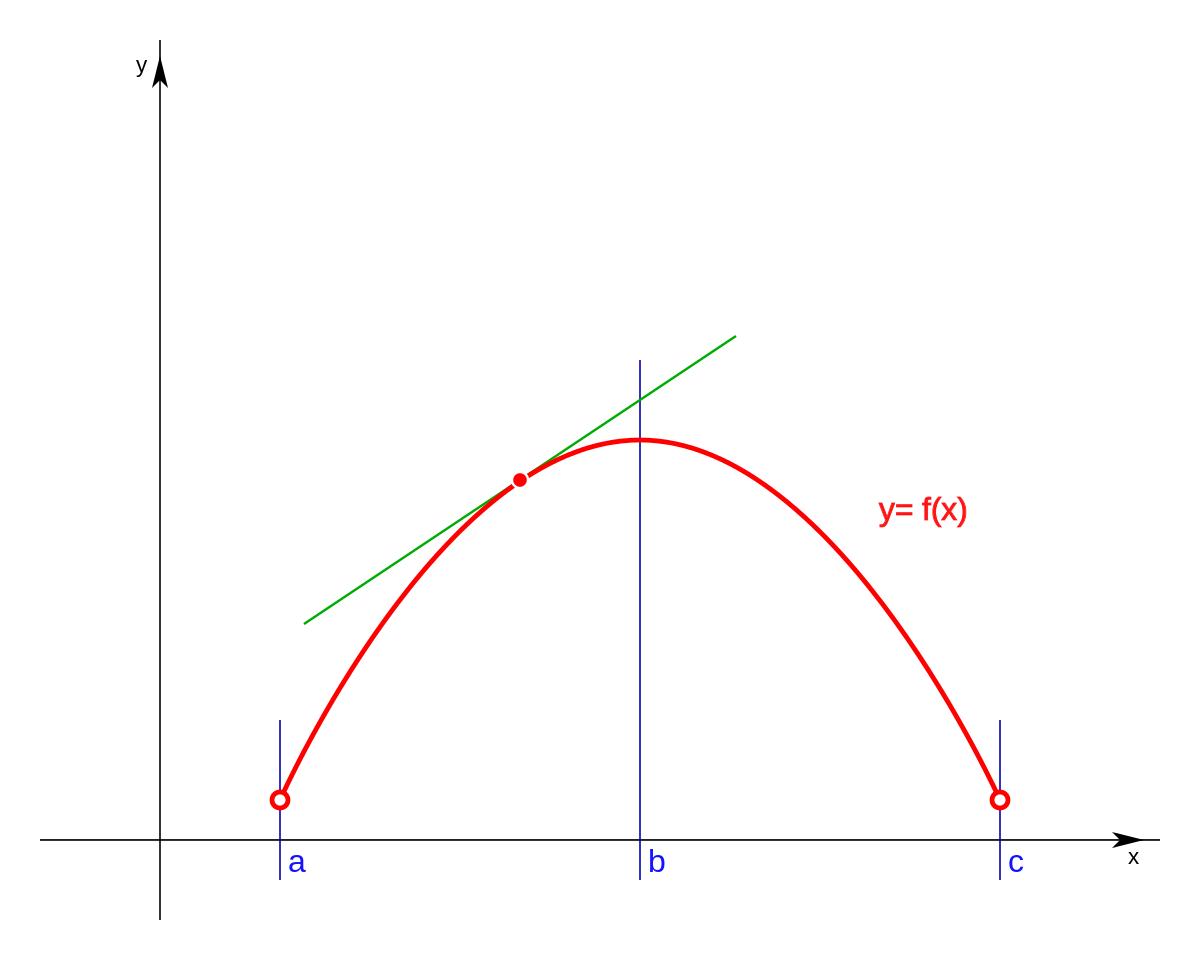
Minima (the plural of 'minimum') of smooth curves occur at turning points, which by definition are also stationary points. A clear definition of smoothing of a 1d signal from scipy cookbook shows you how it works. A curve $\gamma\colon i \to \mathbb{r}^n$ is smooth iff it is $c^\infty$ (or $c^p$ for some authors).

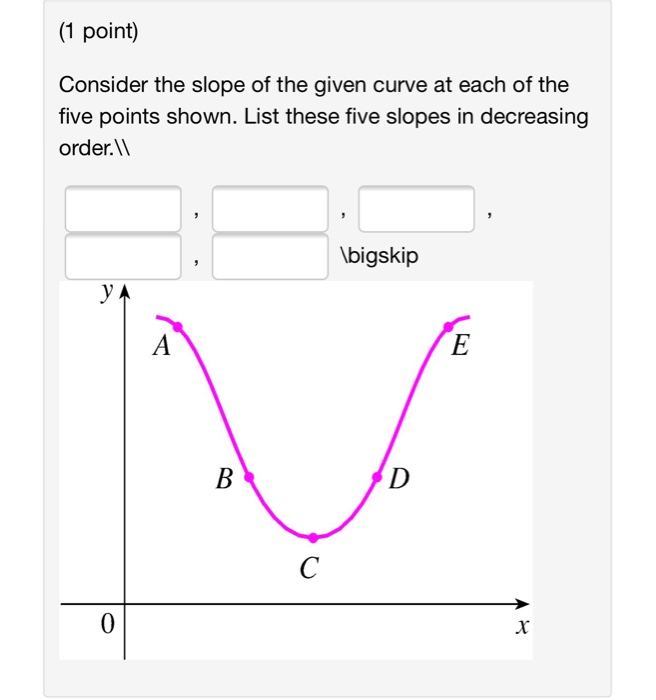
Slope to the right of the origin? F(x1,., xm) = (f1(x1,.,xm) ,., fn(x1,.,xm)) from an open set in one euclidean space into another euclidean space is said to be smooth (or of class c∞) if it. To find the “slope of a curve at a point,” devyn and riley spoke of “zooming in” on a curve until it looks like a line.