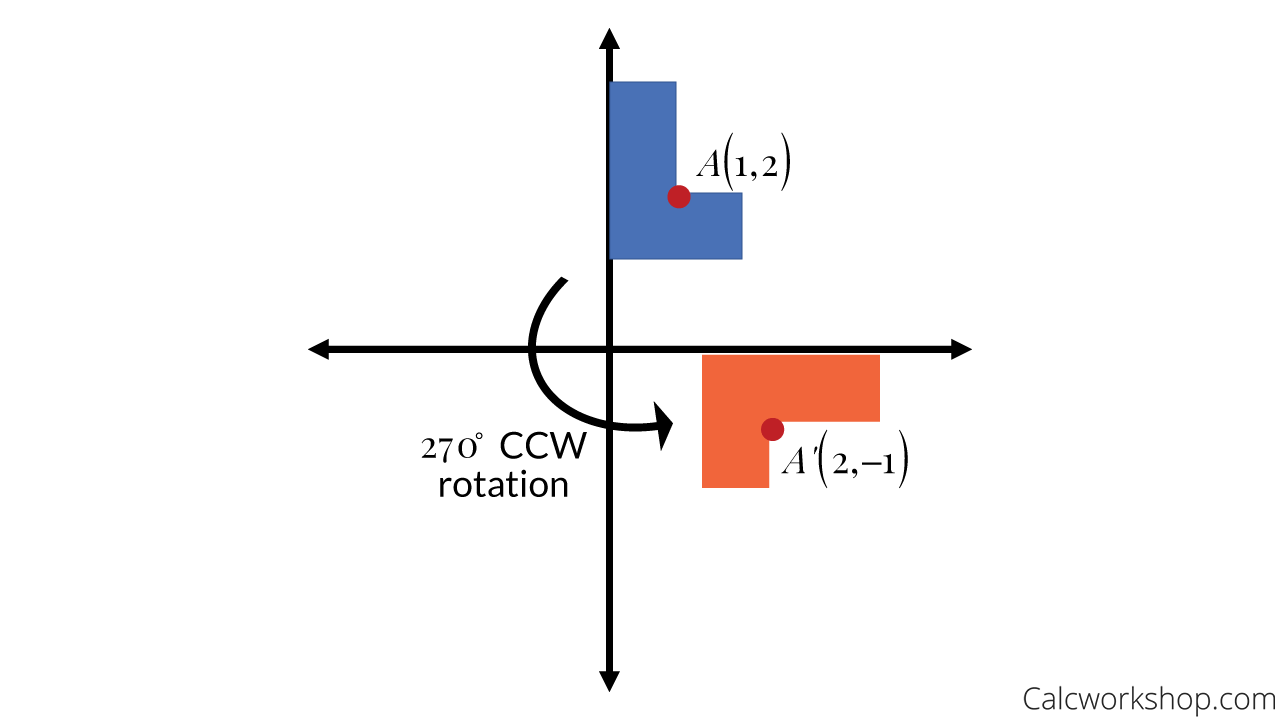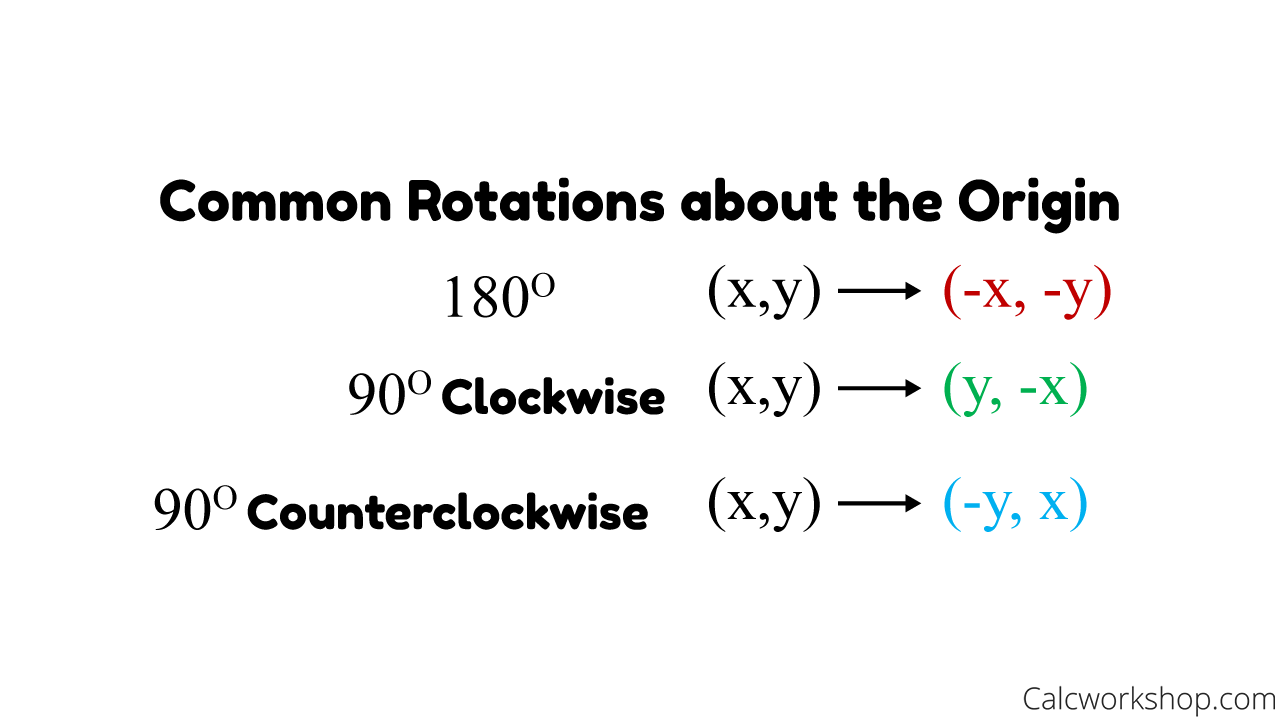One Of The Best Tips About How Do You Rotate Xy Coordinates Dual Axis Line Chart
You are rotating the coordinate axes, not the points.
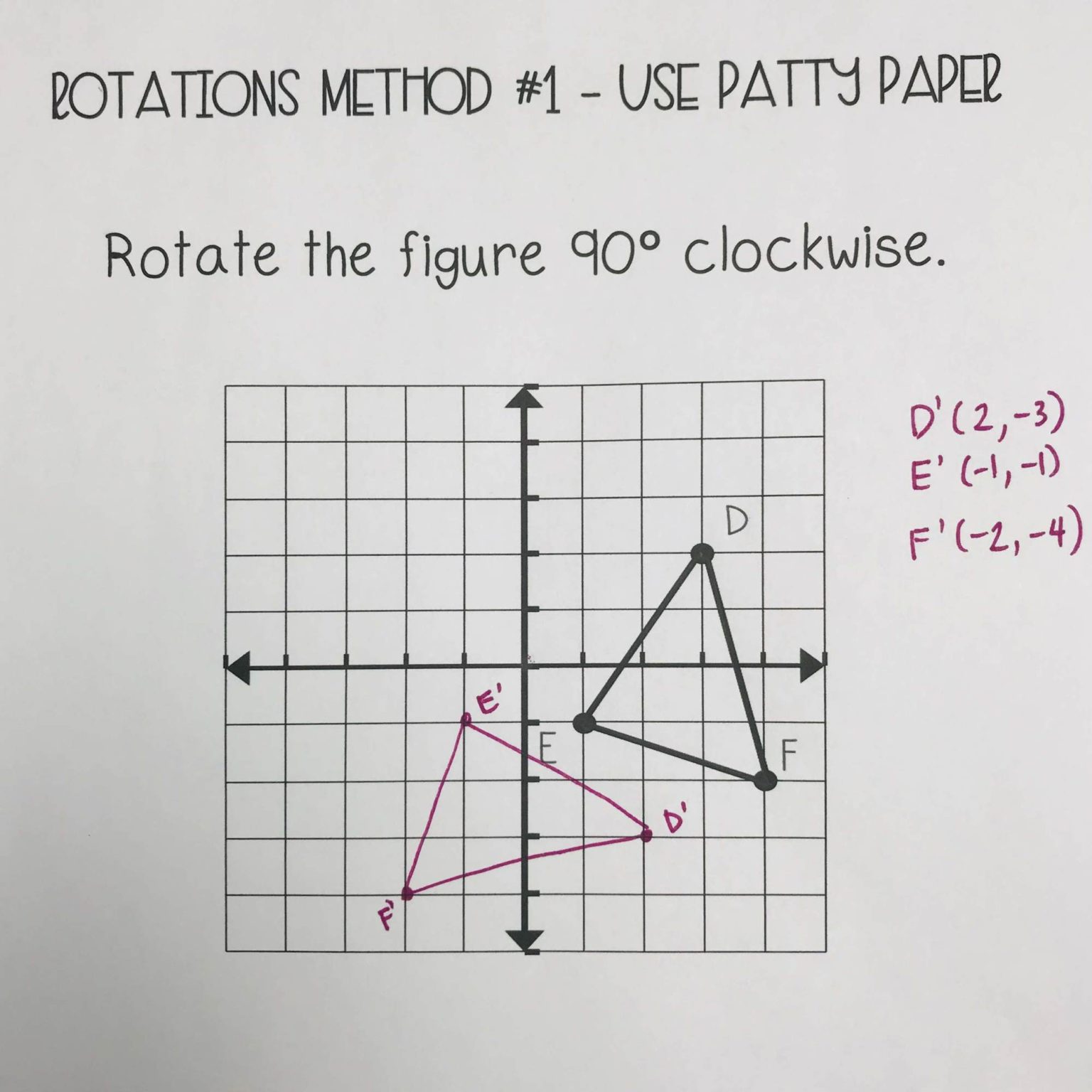
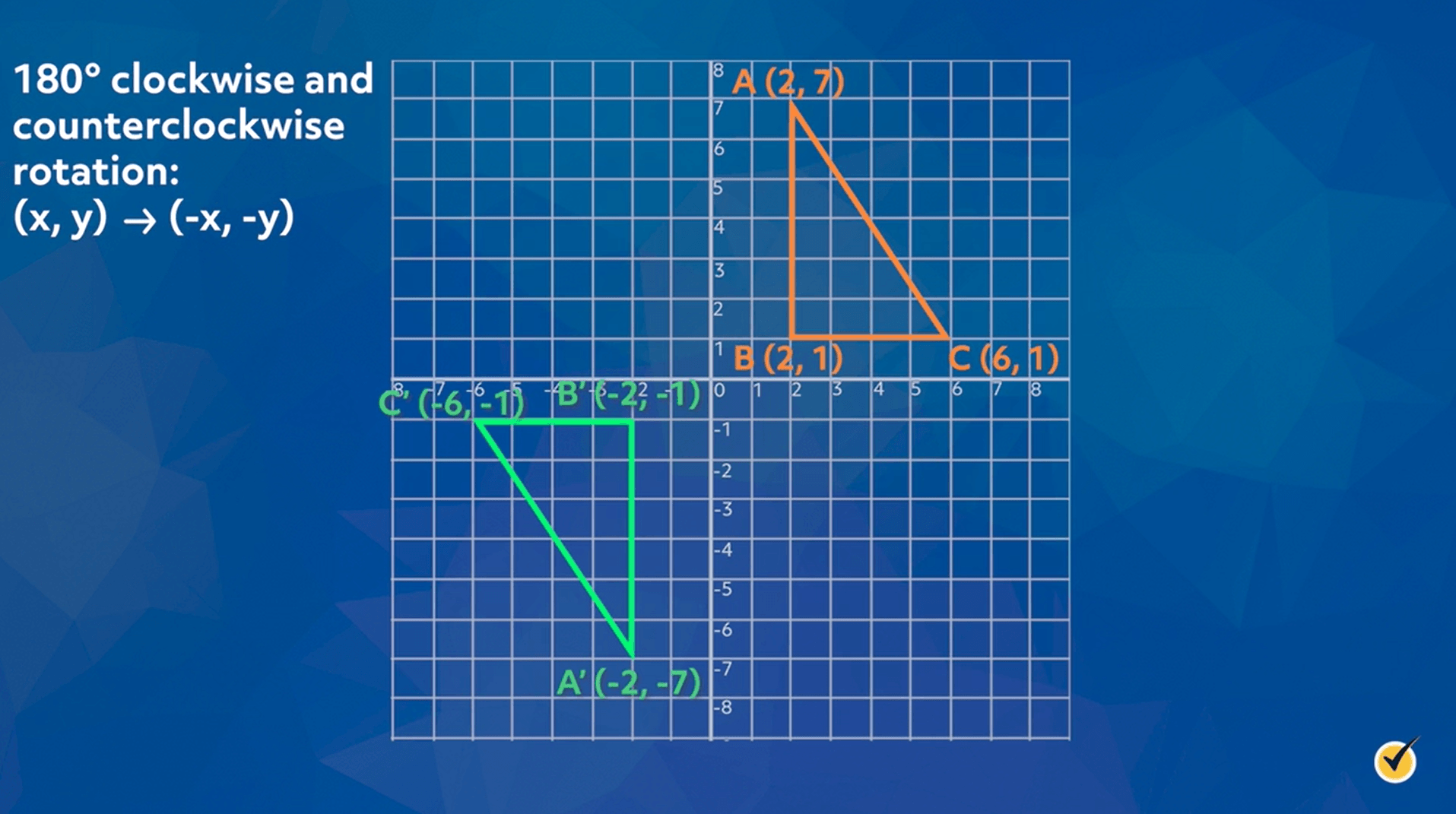
How do you rotate xy coordinates. A rotation of 360 degrees about the origin is equivalent to a rotation of 0 degrees and both are equivalent to the coordinate transformation (𝑥, 𝑦) → (𝑥, 𝑦). If you wanted to rotate that point around the origin, the coordinates of the new point would be located at (x',y'). The point of rotation can be inside or outside of the figure.
In this video, you will learn how to do a rotation graphically and numerically, using the coordinates. Where θ is the angle of rotation. Let $(x,y)$ be a point in the plane.
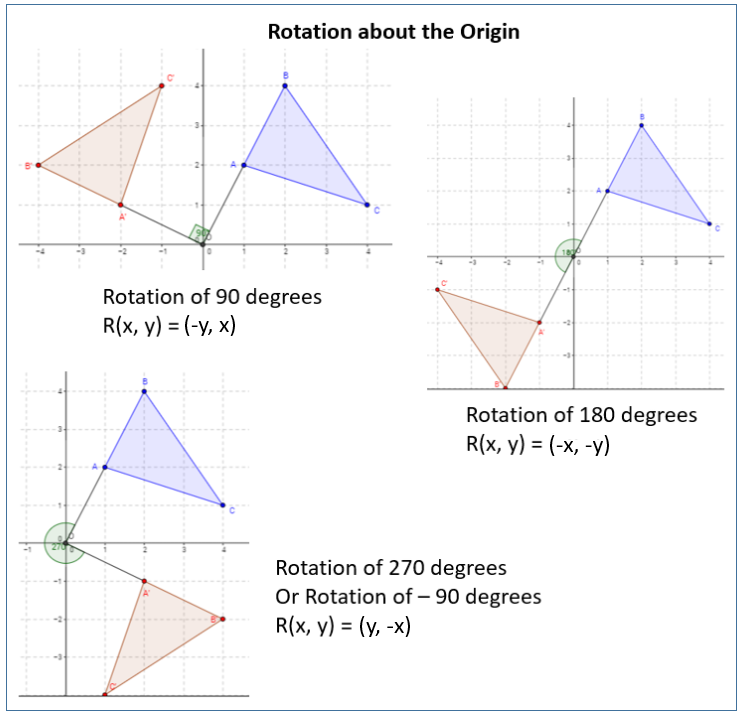
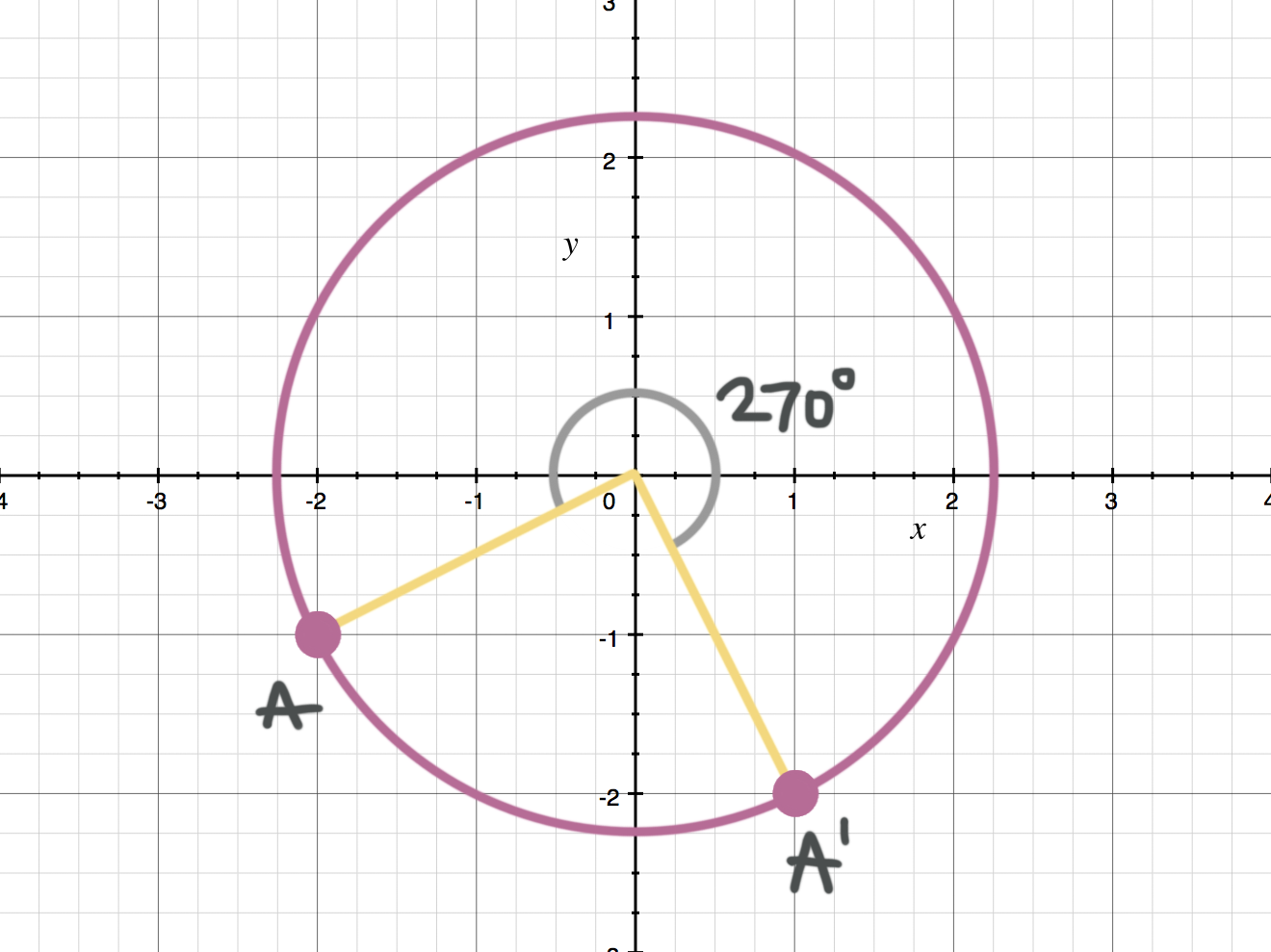
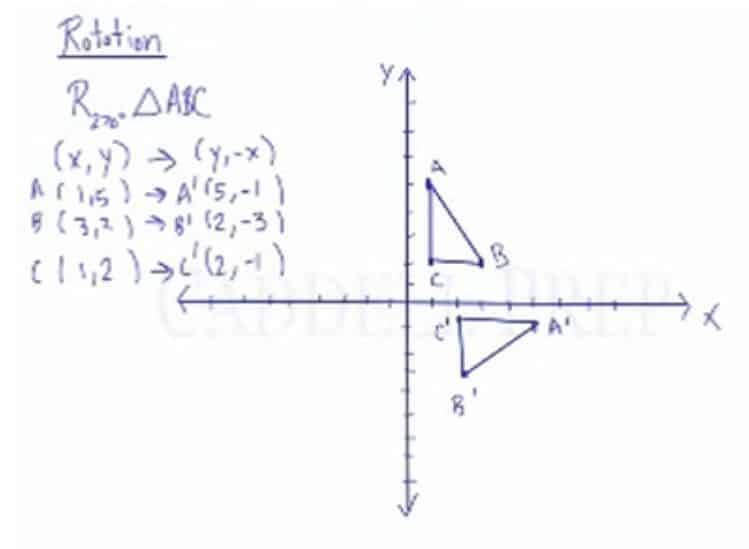
Suppose p = (x, y, z) p = ( x, y, z) a point in 3d 3 d. Apply a rotation of 270 degrees to triangle abc with points a (1,5), b (3,2), and c (1,2). R 90, r 180, and r 270, where the rotation is always counterclockwise.
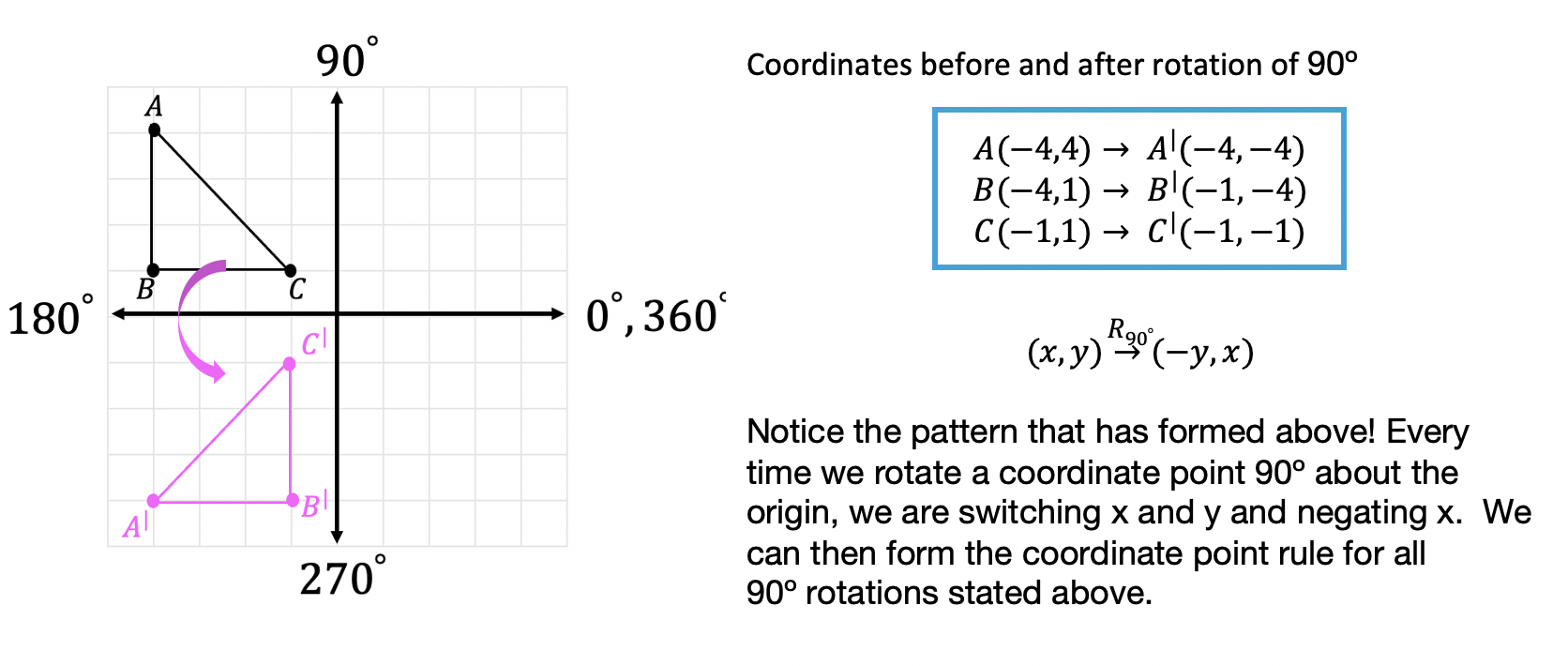
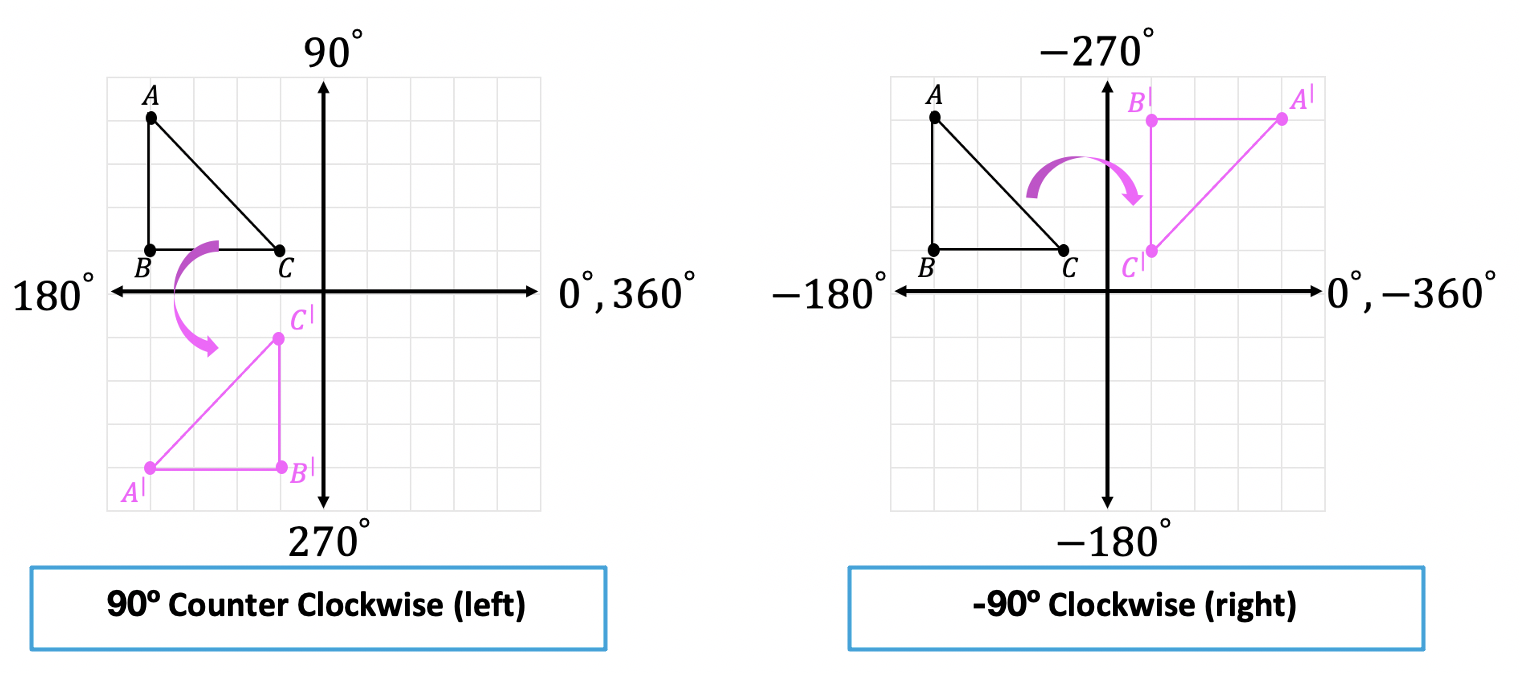
When you rotate by 90 degrees, you take your original x and y, swap them, and make y negative. A rotation of 270 degrees counterclockwise about the origin is equivalent to the coordinate transformation (𝑥, 𝑦) → (𝑦, − 𝑥). And x^ = xcos +ysin and ^y = −xsin +ycos :
To describe a rotation, you need three things: The test could give us coordinates of any one point and asks to find the coordinate of the new rotated point. Note that this rotation does not change the z z coordinate of p p, and that the image of the x x and y y coordinates follow that of the usual 2d 2 d rotation.
The angle between x_ref, y_ref and x_fixed, y_fixed is used to rotate the points (displayed as the black vector in the initial distribution figure). My first post question is: X ′ = x cos.
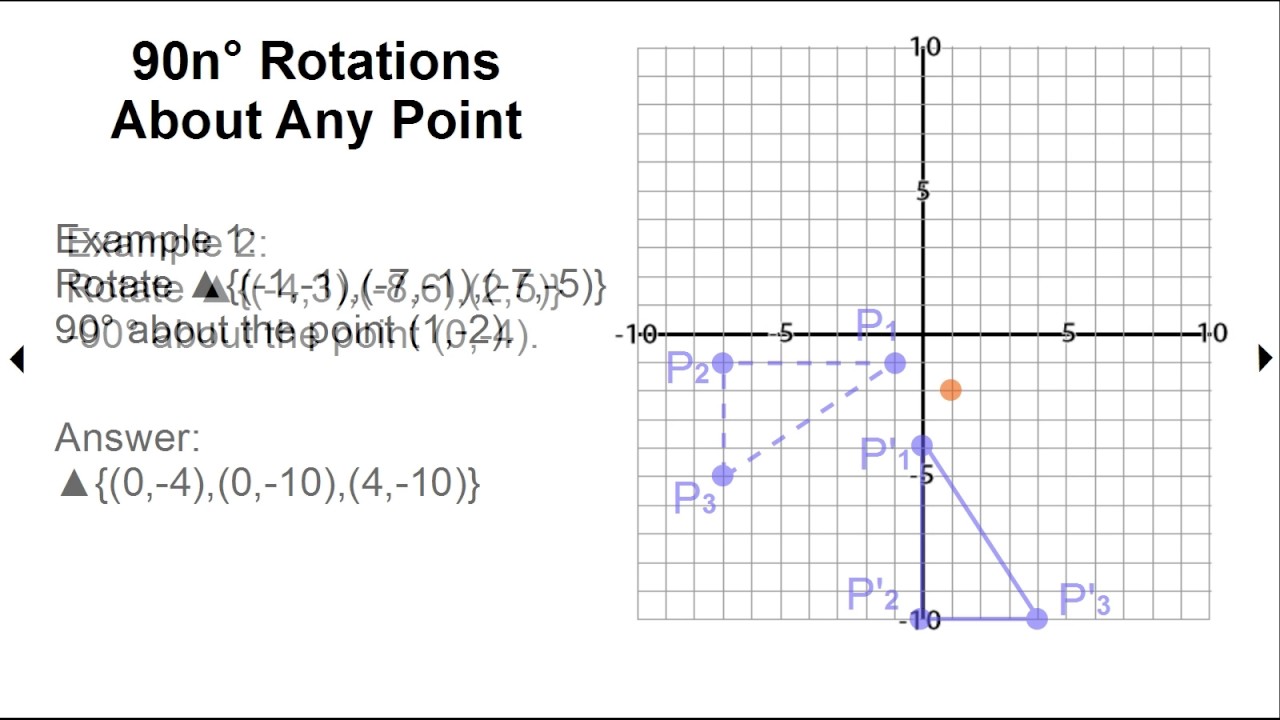
Then i need to calculate the new coordinates after the rotation. For more free magoosh math content visit: Center point of rotation (turn about what point?)
Equations of rotation. We want to rotate p p about the z z axis. Direction (clockwise cw or counterclockwise ccw) angle in degrees;
A rotation is a type of transformation that moves a figure around a central rotation point, called the point of rotation. Θ y ′ = y cos. Imagine a point located at (x,y).
In this lesson we’ll look at how the rotation of a figure in a coordinate plane determines where it’s located. A rotation is an isometric transformation that turns every point of a figure through a specified angle and direction about a fixed point.




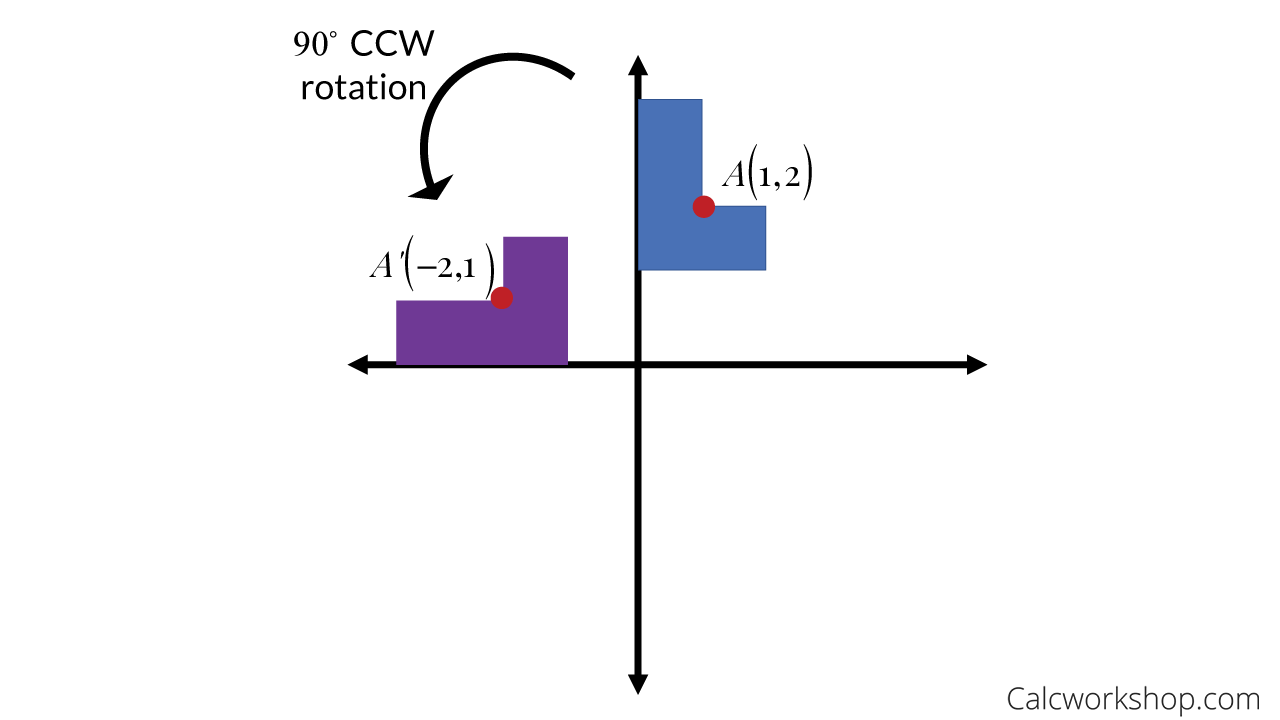
![[Math] Which direction is clockwise when rotating around xaxis in 3D](https://i.stack.imgur.com/fAKih.png)

![How to Rotate a Figure 90 Degrees Clockwise About a Point [Solved]](https://d138zd1ktt9iqe.cloudfront.net/media/seo_landing_files/rotate-a-figure-90-degrees-clockwise-1630331224.png)

![Graph Points & XY Coordinates in the Cartesian Plane [6413] YouTube](https://i.ytimg.com/vi/_521Kngg9ls/maxresdefault.jpg)