Divine Info About How Do You Tell If A Curved Line Is Function To Make Graph In Excel

What are linear functions and families of linear functions?

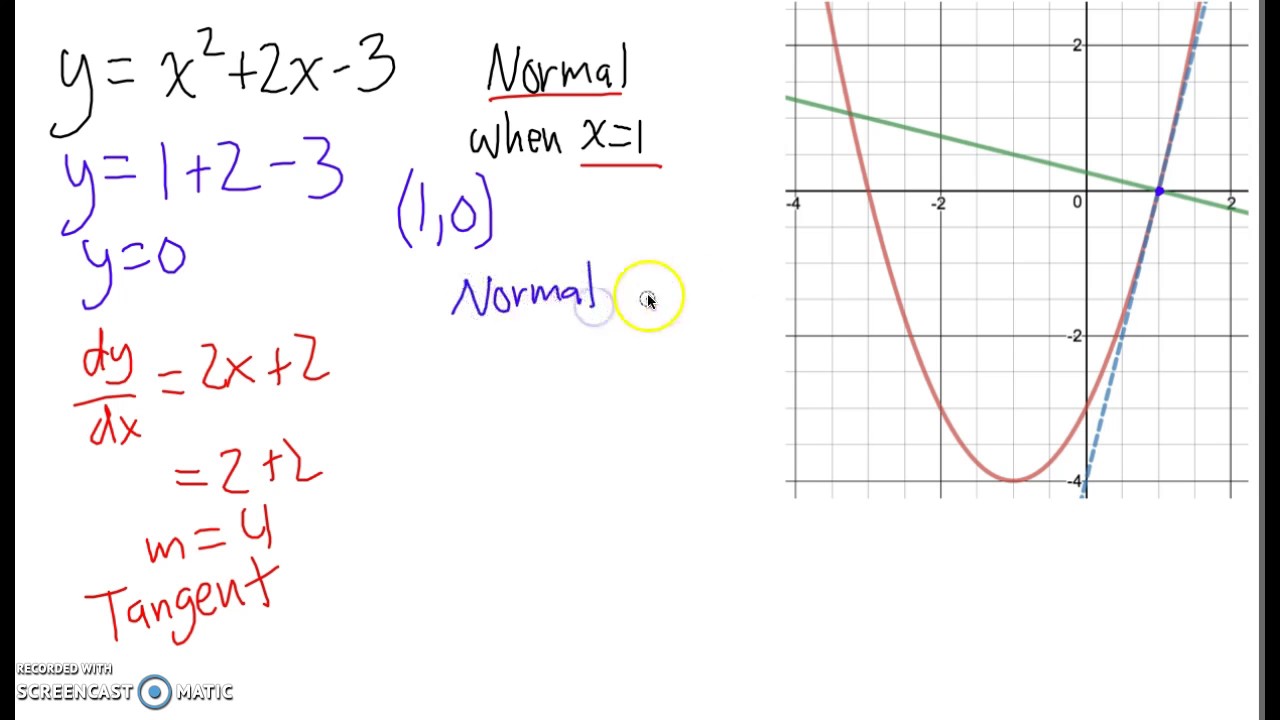
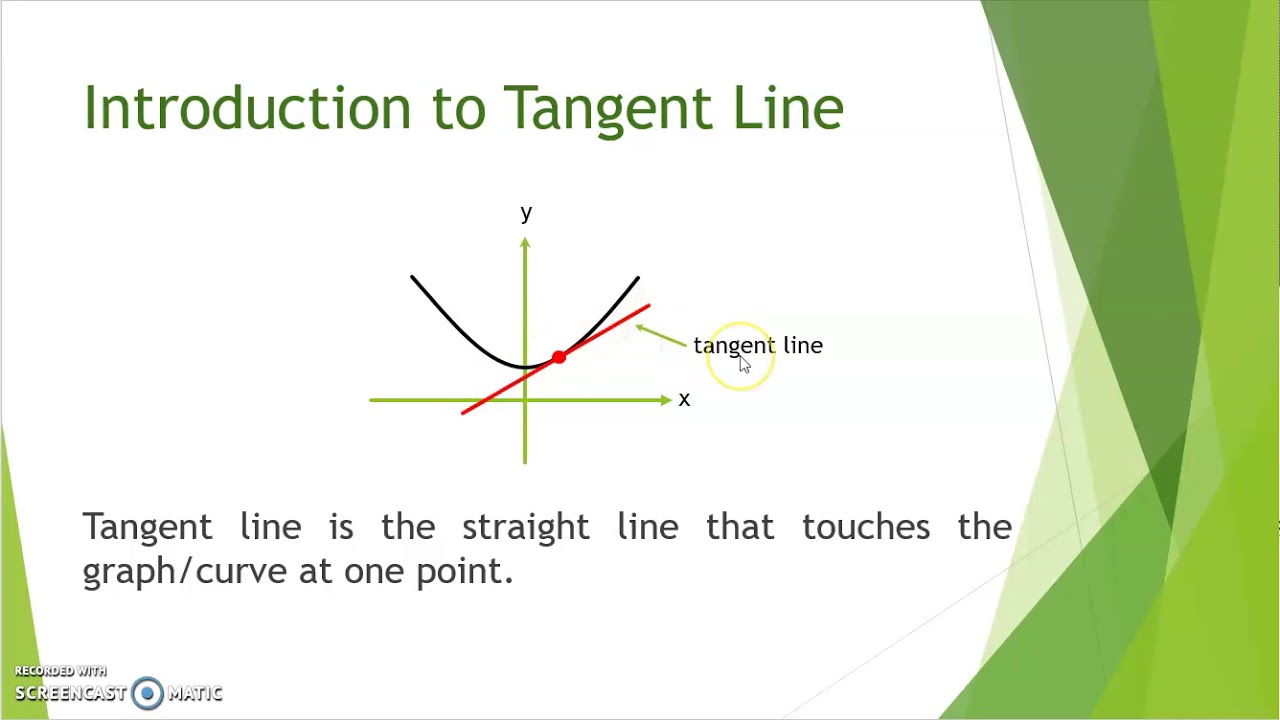
How do you tell if a curved line is a function. Ideally, it is smooth and continuous. The tangent line to a curve at a given point is a straight line that just touches the curve at that point. Select all the intervals where f ′ ( x).

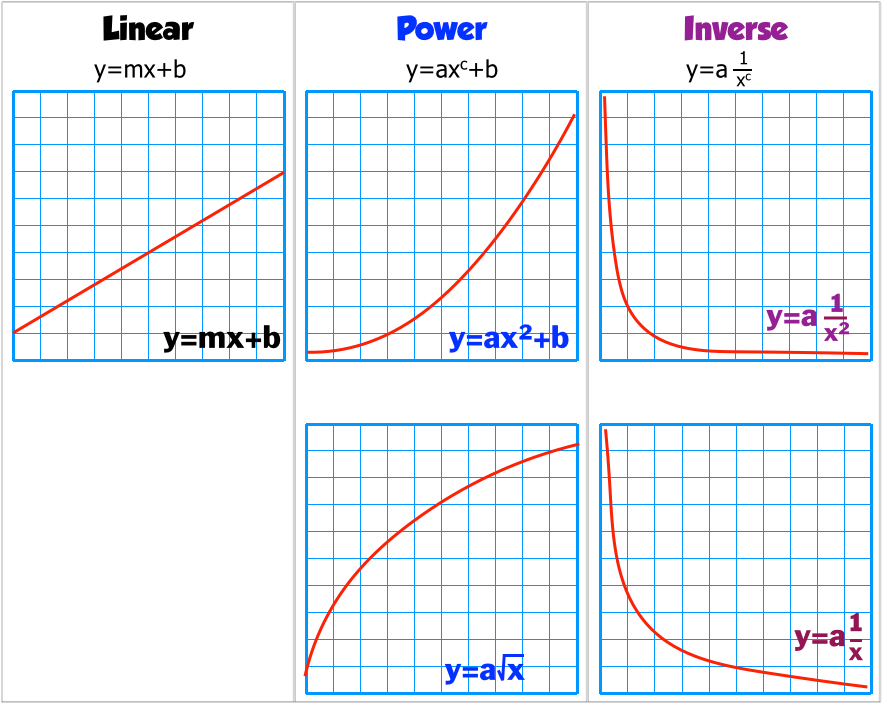
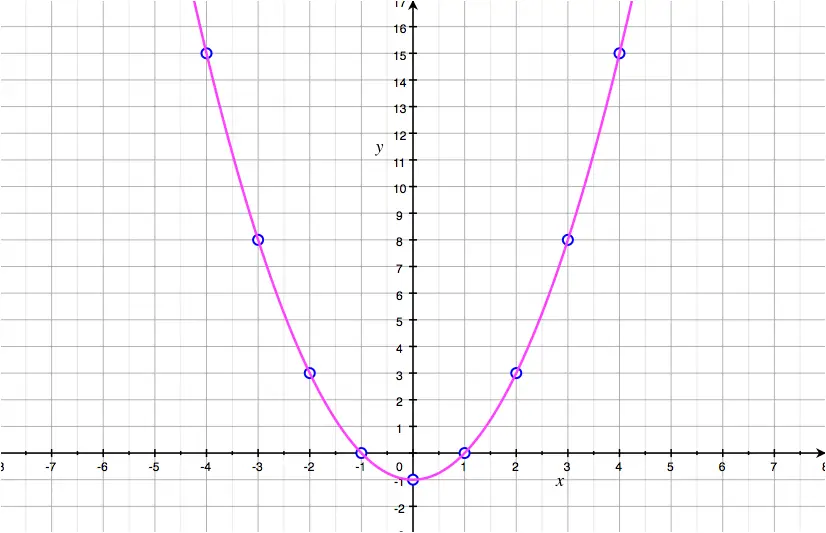
What is the slope of a line? That literally makes zero sense to me. When a function is linear, it forms a straight line when the x and y coordinates are plotted on the cartesian plane.

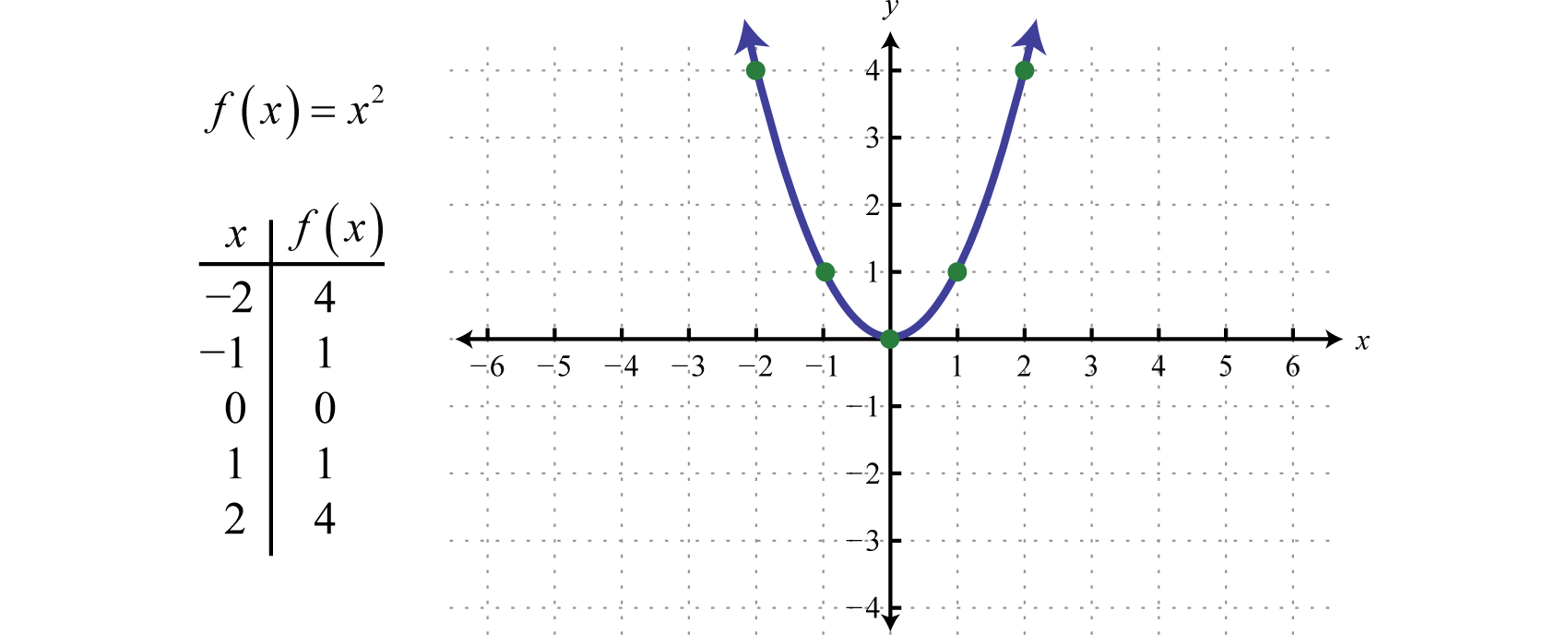
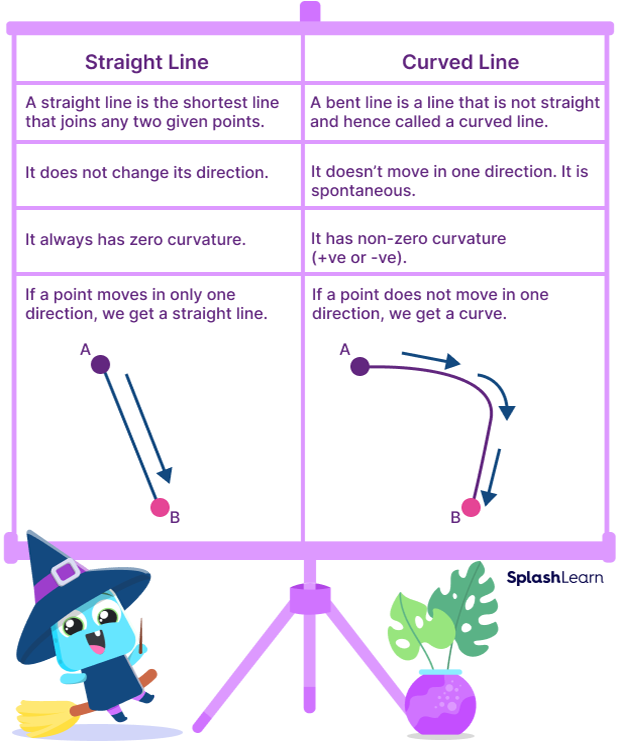
In other words, a curve is defined as a group of points that resemble a straight line that. A linear function is a function that represents a straight line on the coordinate plane. These results demonstrate an unanticipated spatial heterogeneity of photosystem biogenesis and repair functions in thylakoid membranes, and reveal the.

It is nonlinear if it forms a curve when the function is plotted. In mathematics, a curved line is a line that bends or turns continuously, changing its direction at every point on its path. However, if it is curved or.

If you’re examining a function ( f (x) ), you. When it's graphically defined like this, you literally say, ok, when x is 4, if i. A good place to start would be to write down the definition of a closed curve, then try to.

Aug 21, 2018 at 13:03. If the line is straight, it is linear. When the second derivative is positive, the function is concave upward.

A curved line is one that is not straight and is bent. Taking the second derivative actually tells us if the slope continually increases or decreases. Want to learn more about concavity and differential calculus?

If the line passes through a positive. I \to x$ where $ i \subset \mathbb{r}$ is an interval and $x$ is a topological space. What is a function and what do we mean by its domain and range?

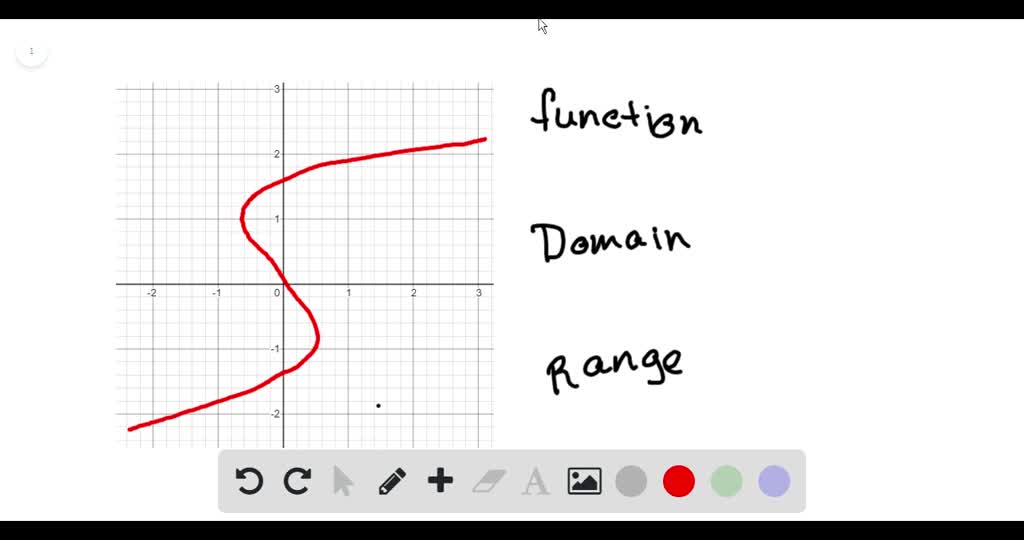
And sometimes there's something called the vertical line test that tells you whether something is a function. Unlike straight lines, curved lines do. Students will often be asked to find the solutions, or the zeros, of these.

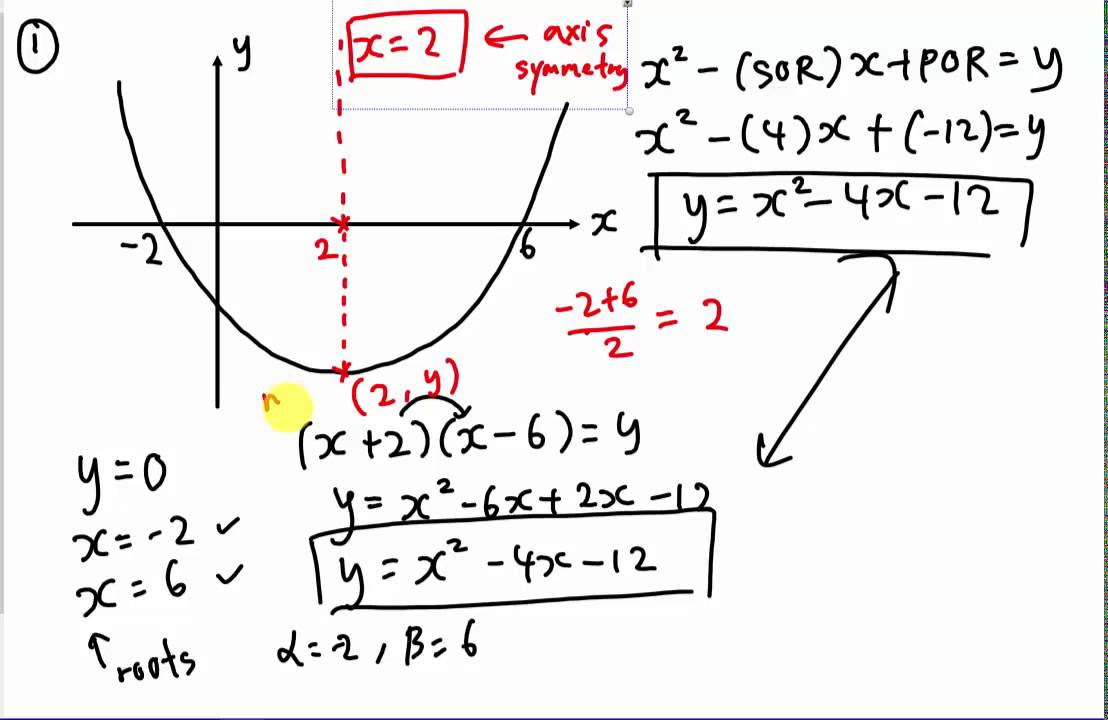
These equations take the form of f (x) = ax^2 + bx + c, and can be solved a variety of ways; A linear function refers to when the dependent variable (usually expressed by 'y') changes by a constant amount as the independent variable (usually 'x') also changes by a. To tell if a function is increasing or decreasing, you should first understand the slope of the function over a given interval.